
【题目】函数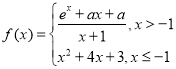 ,则关于x的方程
,则关于x的方程![]() 的实数解最多有( )
的实数解最多有( )
A.7个B.10个C.12个D.15个
【答案】C
【解析】
判断![]() 的单调性,作出
的单调性,作出![]() 的大致函数图象,求出
的大致函数图象,求出![]() 的解,再根据
的解,再根据![]() 的图象得出
的图象得出![]() 的解得个数即可得出结论.
的解得个数即可得出结论.
当![]() 时,
时,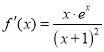
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
∴当![]() 时,
时,![]() 取得极小值
取得极小值![]() .
.
当![]() 时,由二次函数性质可知
时,由二次函数性质可知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴当![]() 时,
时,![]() 取得极小值
取得极小值![]() .
.
当![]() 时,则
时,则![]() 有4个解,不妨设从小到大依次为
有4个解,不妨设从小到大依次为![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
再令![]() ,作出
,作出![]() 的函数图象如图所示:
的函数图象如图所示:
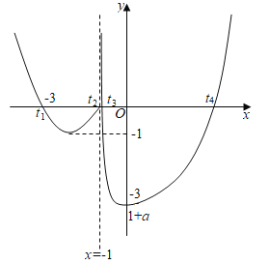
![]() ,则
,则![]() ,(
,(![]() =1,2,3,4).
=1,2,3,4).
由图象可知![]() 有2解,
有2解,![]() 有3解,
有3解,![]() 有4解,
有4解,![]() 有3解,
有3解,
此时![]() 有12解.
有12解.
当![]() 时,则
时,则![]() 有4个解,
有4个解,![]()
则![]() 有3解,
有3解,![]() 至多3解,
至多3解,![]() 至多1解,
至多1解,![]() 至多4解.
至多4解.
此时方程![]() 至多11解.
至多11解.
当![]() 时,则
时,则![]() 有2个解,
有2个解,![]() ,
,
由上可知![]() 无实数根,
无实数根,![]() 有1解,所以
有1解,所以![]() 有1解.
有1解.
当![]() 时,则
时,则![]() 有3个解,
有3个解,![]() ,
,
由上可知![]() 无实数根,
无实数根,![]() 有1解,
有1解, ![]() 有4解.
有4解.
所以此时![]() 有5解.
有5解.
综上所述:![]() 至多12解.
至多12解.
故选:C.


科目:高中数学 来源: 题型:
【题目】设min{m,n}表示m,n二者中较小的一个,已知函数f(x)=x2+8x+14,g(x)=![]() (x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
(x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
A.-4B.-3C.-2D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知圆![]() 过以下4个不同的点:
过以下4个不同的点:![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)先将圆![]() 向左平移
向左平移![]() 个单位后,再将所有点的横坐标、纵坐标都伸长到原来的
个单位后,再将所有点的横坐标、纵坐标都伸长到原来的![]() 倍得到圆
倍得到圆![]() ,若
,若![]() 两个点分别在直线
两个点分别在直线![]() 和
和![]() 上,
上,![]() 为圆
为圆![]() 上任意一点,且
上任意一点,且![]() (
(![]() 为常数),证明直线
为常数),证明直线![]() 过圆
过圆![]() 的圆心,并求
的圆心,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点 和点
和点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),直线l的参数方程为
为参数),直线l的参数方程为![]() (t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,射线m:
(t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,射线m:![]() .
.
(1)求C和l的极坐标方程;
(2)设m与C和l分别交于异于原点的A,B两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提高产品质量,某企业质量管理部门经常不定期地抽查产品进行检测,现在某条生产线上随机抽取100个产品进行相关数据的对比,并对每个产品进行综合评分(满分100分),将每个产品所得的综合评分制成如图所示的频率分布直方图.记综合评分为80分及以上的产品为一等品.
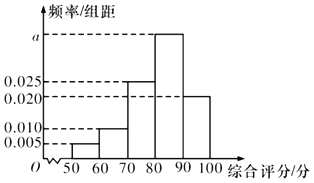
(1)求图中![]() 的值,并求综合评分的中位数;
的值,并求综合评分的中位数;
(2)用样本估计总体,以频率作为概率,按分层抽样的思想,先在该条生产线中随机抽取5个产品,再从这5个产品中随机抽取2个产品记录有关数据,求这2个产品中恰有一个一等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】谢宾斯基三角形是一种分形,由波兰数学家谢宾斯基在1915年提出,先作一个正三角形.挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的小三角形中又挖去一个“中心三角形”,我们用白色代表挖去的面积,那么黑三角形为剩下的面积(我们称黑三角形为谢宾斯基三角形).向图中第5个大正三角形中随机撒512粒大小均匀的细小颗粒物,则落在白色区域的细小颗粒物的数量约是( )

A.256B.350C.162D.96
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com