
【题目】(1)讨论函数f (x)=x+![]() -2的单调性;
-2的单调性;
(2)证明:函数g (x)=![]() -lnx有极小值点x0,且g (x0)∈(0,
-lnx有极小值点x0,且g (x0)∈(0,![]() ).
).
【答案】(1)在(-∞,-![]() ) ,(
) ,(![]() ,+∞)单调递增,在(-
,+∞)单调递增,在(-![]() ,0) ,(0,
,0) ,(0,![]() ) 单调递减.
) 单调递减.
(2)见解析.
【解析】
(1)对函数求导,对![]() 分成
分成![]() 和
和![]() 两类,讨论函数的单调区间.(2)对函数
两类,讨论函数的单调区间.(2)对函数![]() 求导,注意到其导函数
求导,注意到其导函数![]() 是递增函数,用二分法判断出导函数有唯一零点,设这个零点为
是递增函数,用二分法判断出导函数有唯一零点,设这个零点为![]() ,即
,即![]() ,由此得到
,由此得到![]() ,化简
,化简![]() ,由(1)可求得
,由(1)可求得![]() 的取值范围.
的取值范围.
(1)f (x)的定义域为(-∞,0)∪(0,+∞),f′(x)=![]() .
.
若a≤0,则f′(x)>0,f (x)在(-∞,0) ,(0,+∞)单调递增.
若a>0,当x<-![]() 或x>-
或x>-![]() 时,f′(x)>0;
时,f′(x)>0;
当-![]() <x<0或0<x<
<x<0或0<x<![]() 时,f′(x)<0.所以f (x)在(-∞,-
时,f′(x)<0.所以f (x)在(-∞,-![]() ) ,(
) ,(![]() ,+∞)单调递增,
,+∞)单调递增,
在(-![]() ,0) ,(0,
,0) ,(0,![]() ) 单调递减.
) 单调递减.
(2)g (x)定义域(0,+∞),g′ (x)=![]() -
-![]() 在 (0,+∞)单调递增.
在 (0,+∞)单调递增.
由g′ (1)=![]() -1<0,g′ (2)=
-1<0,g′ (2)=![]() >0,故g′ (x)在(0,+∞)存在唯一零点x0,且x0∈(1,2).
>0,故g′ (x)在(0,+∞)存在唯一零点x0,且x0∈(1,2).
当x∈(1,x0)时,g′ (x)<0;当x∈(x0,+∞)时,g′ (x)>0.所以g (x)≥g (x0).
又由g′ (x0)=0,可得![]() =
=![]() ,所以lnx0=2-x0.
,所以lnx0=2-x0.
可得g (x0)=x0+![]() -2,由(1)知g (x0)=x0+
-2,由(1)知g (x0)=x0+![]() -2在(1,2)单调递增,所以g (x0) ∈(0,
-2在(1,2)单调递增,所以g (x0) ∈(0,![]() ).
).


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】若从装有![]() 个红球和
个红球和![]() 个黑球的口袋内任取
个黑球的口袋内任取![]() 个球,则下列为互斥的两个事件是( )
个球,则下列为互斥的两个事件是( )
A.“至少有一个黑球”与“都是黑球”B.“一个红球也没有”与“都是黑球”
C.“至少有一个红球”与“都是红球”D.“恰有![]() 个黑球”与“恰有
个黑球”与“恰有![]() 个黑球”
个黑球”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家外卖公司,其“骑手”的日工资方案如下:甲公司规定底薪70元,每单抽成1元;乙公司规定底薪100元,每日前45单无抽成,超出45单的部分每单抽成6元.
假设同一公司的“骑手”一日送餐单数相同,现从两家公司各随机抽取一名“骑手”并记录其100天的送餐单数,得到如下条形图:

(Ⅰ)求乙公司的“骑手”一日工资y(单位:元)与送餐单数n(n∈N﹡)的函数关系;
(Ⅱ)若将频率视为概率,回答以下问题:
(i)记乙公司的“骑手”日工资为X(单位:元),求X的分布列和数学期望;
(ⅱ)小明拟到这两家公司中的一家应聘“骑手”的工作,如果仅从日工资的角度考虑,请你利用所学的统计学知识为他做出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=![]() ,AC=3, BC=2,P是△ABC内的一点.
,AC=3, BC=2,P是△ABC内的一点.

(1)若△BPC是以BC为斜边的等腰直角三角形,求PA长;
(2)若∠BPC=![]() ,求△PBC面积的最大值.
,求△PBC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解所经销商品的使用情况,随机问卷50名使用者,然后根据这50名的问卷评分数据,统计得到如图所示的频率布直方图,其统计数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求频率分布直方图中a的值并估计这50名使用者问卷评分数据的中位数;
(2)从评分在[40,60)的问卷者中,随机抽取2人,求此2人评分都在[50,60)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某支上市股票在30天内每股的交易价格![]() (单位:元)与时间
(单位:元)与时间![]() (单位:天)组成有序数对
(单位:天)组成有序数对![]() ,点
,点![]() 落在如图所示的两条线段上.该股票在30天内(包括30天)的日交易量
落在如图所示的两条线段上.该股票在30天内(包括30天)的日交易量![]() (单位:万股)与时间
(单位:万股)与时间![]() (单位:天)的部分数据如下表所示:
(单位:天)的部分数据如下表所示:
第 | 4 | 10 | 16 | 22 |
| 36 | 30 | 24 | 18 |

(Ⅰ)根据所提供的图象,写出该种股票每股的交易价格![]() 与时间
与时间![]() 所满足的函数解析式;
所满足的函数解析式;
(Ⅱ)根据表中数据确定日交易量![]() 与时间
与时间![]() 的一次函数解析式;
的一次函数解析式;
(Ⅲ)若用![]() (万元)表示该股票日交易额,请写出
(万元)表示该股票日交易额,请写出![]() 关于时间
关于时间![]() 的函数解析式,并求出在这30天中,第几天的日交易额最大,最大值是多少?
的函数解析式,并求出在这30天中,第几天的日交易额最大,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①![]() 中,
中,![]() 是
是![]() 成立的充要条件;
成立的充要条件;
②当![]() 时,有
时,有![]() ;
;
③已知![]() 是等差数列
是等差数列![]() 的前n项和,若
的前n项和,若![]() ,则
,则![]() ;
;
④若函数![]() 为
为![]() 上的奇函数,则函数
上的奇函数,则函数![]() 的图象一定关于点
的图象一定关于点![]() 成中心对称.其中所有正确命题的序号为___________.
成中心对称.其中所有正确命题的序号为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在实数对
,若存在实数对![]() ,使得等式
,使得等式![]() 对定义域中的任意
对定义域中的任意![]() 都成立,则称函数
都成立,则称函数![]() 是“
是“![]() 型函数”.
型函数”.
(1)若函数![]() 是“
是“![]() 型函数”,且
型函数”,且![]() ,求出满足条件的实数对
,求出满足条件的实数对![]() ;
;
(2)已知函数![]() .函数
.函数![]() 是“
是“![]() 型函数”,对应的实数对
型函数”,对应的实数对![]() 为
为![]() ,当
,当![]() 时,
时,![]() .若对任意
.若对任意![]() 时,都存在
时,都存在![]() ,使得
,使得![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.2018年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本2500万元,每生产x(百辆),需另投入成本![]() 万元,且
万元,且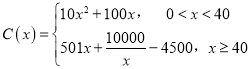 .由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.
.由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.
(1)求出2018年的利润L(x)(万元)关于年产量x(百辆)的函数关系式;(利润=销售额-成本)
(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com