
����Ŀ����ƽ��ֱ������ϵxOy�У���֪C1�� ![]() ����Ϊ����������C1�ϵ����е�ĺ����ꡢ������ֱ��쳤Ϊԭ����
����Ϊ����������C1�ϵ����е�ĺ����ꡢ������ֱ��쳤Ϊԭ���� ![]() ��2����õ�����C2��ƽ��ֱ������ϵxOy��ԭ��OΪ���㣬x���������Ϊ���ᣬȡ��ͬ�ĵ�λ���Ƚ���������ϵ����ֱ֪��l���ѣ�
��2����õ�����C2��ƽ��ֱ������ϵxOy��ԭ��OΪ���㣬x���������Ϊ���ᣬȡ��ͬ�ĵ�λ���Ƚ���������ϵ����ֱ֪��l���ѣ� ![]() cos��+sin�ȣ�=4
cos��+sin�ȣ�=4
��1����д������C1�ļ����귽��������C2�IJ������̣�
��2��������C2����һ��P��ʹ��P��ֱ��l�ľ�����С���������Сֵ��
���𰸡�
��1���⣺��C1�� ![]() ����Ϊ����������ȥ������Ϊ��ͨ����Ϊ x2+y2=1��
����Ϊ����������ȥ������Ϊ��ͨ����Ϊ x2+y2=1��
������C1���ļ����귽��Ϊ��=1��
�ٸ��ݺ���ͼ��������任���ɿɵ�����C2����ͨ����Ϊ  +
+ ![]() =1����
=1���� ![]() +
+ ![]() =1��
=1��
������C2�ļ���������Ϊ 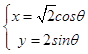 ����Ϊ������
����������
��2���⣺ֱ��l���ѣ� ![]() cos��+sin�ȣ�=4����
cos��+sin�ȣ�=4���� ![]() x+y��4=0�����P��
x+y��4=0�����P�� ![]() cos�ȣ�2sin�ȣ���
cos�ȣ�2sin�ȣ���
���P��ֱ�ߵľ���Ϊd= ![]() =
=  ��
��
�ʵ�sin����+ ![]() ��=1ʱ��dȡ����Сֵ����ʱ����=2k��+
��=1ʱ��dȡ����Сֵ����ʱ����=2k��+ ![]() ��k��z����P��1��
��k��z����P��1�� ![]() ����
����
������C2����һ��P��1�� ![]() �����㵽ֱ��l�ľ������СֵΪ
�����㵽ֱ��l�ľ������СֵΪ ![]() ��
�� ![]()
����������1����C1��ȥ������Ϊ��ͨ����Ϊ x2+y2=1���ٻ�Ϊ�����귽�̣����ݺ���ͼ��������任���ɿɵ�����C2����ͨ���̣��ٻ�Ϊ���������̣���2�������ֱ��l��ֱ�����귽�̣����P�� ![]() cos�ȣ�2sin�ȣ�����õ�P��ֱ�ߵľ���Ϊd=
cos�ȣ�2sin�ȣ�����õ�P��ֱ�ߵľ���Ϊd= ![]() ���ʵ�sin����+
���ʵ�sin����+ ![]() ��=1ʱ������=2k��+
��=1ʱ������=2k��+ ![]() ��k��zʱ����P��ֱ��l�ľ������Сֵ���Ӷ����P�������Լ�����Сֵ
��k��zʱ����P��ֱ��l�ľ������Сֵ���Ӷ����P�������Լ�����Сֵ


 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д� �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ü��������120������������������λ���֣��磺34�����λ����Ϊ3��567�����λ����Ϊ5����Ƶ���ֲ�ͼ��ͼ��ʾ��������120��������������ȡ��һ�����������λ����Ϊd��d=1��2������9���ĸ���ΪP������ѡ���У����ܷ�ӳP��d�Ĺ�ϵ���ǣ� �� 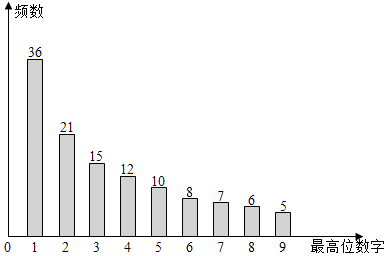
A.P=lg��1+ ![]() ��
��
B.P= ![]()
C.P= ![]()
D.P= ![]() ��
�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��| ![]() |=1��|
|=1��| ![]() |=
|= ![]() ��
�� ![]()
![]() =0����C�ڡ�AOB�ڣ��ҡ�AOC=30�㣬��
=0����C�ڡ�AOB�ڣ��ҡ�AOC=30�㣬�� ![]() =m
=m ![]() +n
+n ![]() ��m��n��R������
��m��n��R������ ![]() ���ڣ� ��
���ڣ� ��
A.![]()
B.3
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��0����2������ԲE�� ![]() +
+ ![]() =1��a��b��0����������Ϊ
=1��a��b��0����������Ϊ ![]() ��F����Բ�Ľ��㣬ֱ��AF��б��Ϊ
��F����Բ�Ľ��㣬ֱ��AF��б��Ϊ ![]() ��OΪ����ԭ�㣮
��OΪ����ԭ�㣮
������E�ķ��̣�
���������A��ֱ��l��E�ཻ��P��Q���㣬����OPQ��������ʱ����l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=sin��2x�� ![]() ��+2cos2x��1��x��R����
��+2cos2x��1��x��R����
��1����f��x���ĵ����������䣻
��2���ڡ�ABC�У����ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c����֪f��A��= ![]() ��b��a��c�ɵȲ����У���
��b��a��c�ɵȲ����У��� ![]()
![]() =9����a��ֵ��
=9����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn �� �㣨n��Sn+3����n��N*���ں���y=3��2x��ͼ���ϣ��ȱ�����{bn}����bn+bn+1=an��n��N*������ǰn���ΪTn �� �����н�����ȷ���ǣ� ��
A.Sn=2Tn
B.Tn=2bn+1
C.Tn��an
D.Tn��bn+1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABC��A1B1C1�У�����ACC1A1�͵���ABC����A1AC=60�㣬AC=2AA1=4����D��E�ֱ���AA1 �� BC���е㣮 
��1��֤����DE��ƽ��A1B1C��
��2����AB=2����BAC=60�㣬��ֱ��DE��ƽ��ABB1A1���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x��2|+|x+4|��g��x��=x2+4x+3��
��1����ʽf��x����g��x���Ľ⼯��
��2����f��x����|1��5a|���������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(��С������12��)
��ͼ��������P��ABCD�У�����ABCD�Ǿ��Σ�PA��ƽ��ABCD��AP=AB��BP=BC=2��E��F�ֱ���PB,PC���е�.
(��)֤����EF��ƽ��PAD��
(��)������E��ABC�����V.

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com