练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是菱形，PD⊥平面ABCD，PD=AD=3，PM=2MD，AN=2NB，∠DAB=60°．

    （1）求证：直线AM∥平面PNC；

    （2）求二面角D﹣PC﹣N的余弦值．

    【答案】（1）见解析；（2）.

    【解析】试题分析：（1）在上取一点，使，连接， ，可得， ， 为平行四边形，即，即可得直线平面．

    （2）取中点，可得， ， 相互垂直，以为原点，如图建立空间直角坐标系，易知平面的法向量，求出面的法向量，计算出两向量夹角即可.

    试题解析：（1）在上取一点，使，连接， ，


    ∵， ，∴， ， ， ∴， ，∴为平行四边形，即，又平面，∴直线平面．

    （2）取中点，底面是菱形， ，∴，∵，∴，即，又平面，∴，又，∴直线平面，故， ， 相互垂直，以为原点，如图建立空间直角坐标系．


    则， ， ， ， ， ，易知平面的法向量，设面的法向量，由，得，∴，故二面角的余弦值为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝|3x－1|－2|x|＋2.

    (Ⅰ)解不等式：f(x)<10；

    (Ⅱ)若对任意的实数x，f(x)－|x|≤a恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线.

    (1)求曲线在点P(2,4)处的切线方程；

    (2)求曲线过点P(2,4)的切线方程；

    (3)求斜率为1的曲线的切线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(导学号：05856290)[选修4－5：不等式选讲]

    已知函数f(x)＝|x－a|＋|x－2a|.

    (Ⅰ)对任意x∈R，不等式f(x)>1成立，求实数a的取值范围；

    (Ⅱ)当a＝－1时，解不等式f(x)<3.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f(x)＝emx＋x2－mx.

    (1)证明：f(x)在(－∞，0)单调递减，在(0，＋∞)单调递增；

    (2)若对于任意x1，x2∈[－1,1]，都有，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形是矩形平面.

    （1）证明：平面平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种产品按质量标准分为,,,,五个等级.现从一批该产品随机抽取20个，对其等级进行统计分析，得到频率分布表如下：

    等级

    频率

    （1）在抽取的20个产品中，等级为5的恰有2个，求,；

    （2）在（1）的条件下，从等级为3和5的所有产品中，任意抽取2个，求抽取的2个产品等级恰好相同的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(导学号：05856301)已知函数f(x)＝m(x－1)ex＋x2(m∈R)，其导函数为f′(x)，若对任意的x<0，不等式x2＋(m＋1)x>f′(x)恒成立，则实数m的取值范围为(　　)

    A. (0,1) B. (－∞，1) C. (－∞，1] D. (1，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

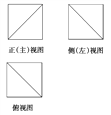
    【题目】如图，已知正方体ABCD－A′B′C′D′的外接球的体积为π，将正方体割去部分后，剩余几何体的三视图如图所示，则剩余几何体的表面积为(　　)

    A. ＋ B. 3＋或＋ C. 3＋ D. ＋或2＋

    查看答案和解析>>

    同步练习册答案