【题目】中国足球甲
联赛共有12个足球俱乐部参加，实行主客场双循环赛制，即任何两队分别在主场和客场各比赛一场，胜一场得3分，平一场各得1分，负一场得0分，在联赛结束后按积分的高低排出名次.则在积分榜上位次相邻的两支球队积分差距最多可达_________分.
科目：高中数学 来源： 题型：
【题目】（1）求与椭圆
有共同焦点且过点
的双曲线的标准方程；
（2）已知抛物线的焦点在
轴上，抛物线上的点
到焦点的距离等于5，求抛物线的标准方程和
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A.棱锥的侧棱长与底面多边形的边长相等，则此棱锥可能是六棱锥
B.四棱锥的四个侧面都可以是直角三角形
C.有两个平面互相平行，其余各面都是梯形的多面体是棱台
D.棱台的各侧棱延长后不一定交于一点
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，在四棱锥S-ABCD中，SA⊥平面ABCD，底面ABCD是梯形，AB//CD，DA⊥AB，BC⊥SC，SA=AD=3，AB=6，点E在棱SD上，且VS-ACE=2VE-ACD。
（1）求证：BC⊥平面SAC；
（2）求二面角S-AE-C的余弦值。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个袋中有2个红球，4个白球.
（1）从中取出3个球，求取到红球个数
的概率分布及数学期望；
（2）每次取1个球，取出后记录颜色并放回袋中.
①若取到第二次红球就停止试验，求第5次取球后试验停止的概率；
②取球4次，求取到红球个数
的概率分布及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，矩形ABCD中，AD⊥平面ABE，AE＝EB＝BC＝2，F为CE上的点，且BF⊥平面ACE.
(1)求证：AE⊥平面BCE；
(2)求证：AE∥平面BFD；
(3)求三棱锥C－BGF的体积．
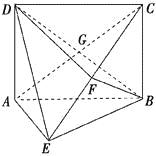
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法：
①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变；
②设有一个回归方程
，变量
增加一个单位时，
平均增加
个单位；
③线性回归方程
必过
)；
④在一个
列联表中，由计算得
，则有
以上的把握认为这两个变量间有关系．
其中错误的个数是( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】现有8名马拉松比赛志愿者，其中志愿者
，
，
通晓日语，
，
，
通晓俄语，
，
通晓英语，从中选出通晓日语、俄语和英语的志愿者各1名，组成一个小组．
列出基本事件；
求被选中的概率；
求和不全被选中的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
