
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)求证:直线![]() 是曲线
是曲线![]() 的切线;
的切线;
(Ⅲ)写出![]() 的一个值,使得函数
的一个值,使得函数![]() 有三个不同零点(只需直接写出数值)
有三个不同零点(只需直接写出数值)
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】如图,已知圆锥的顶点为P,母线长为4,底面圆心为O,半径为2.

(1)求这个圆锥的体积;
(2)设OA,OB是底面半径,且∠AOB=90°,M为线段AB的中点,求异面直线PM与OB所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() .
.
(Ⅰ)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ,令
,令![]() ,求
,求![]() 的解析式及其最小值(注:
的解析式及其最小值(注:![]() 为自然对数的底数).
为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度![]() (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度![]() (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到![]() 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为![]() ;当车流密度不超过
;当车流密度不超过![]() 辆/千米时,车流速度为
辆/千米时,车流速度为![]() 千米/小时,研究表明:当
千米/小时,研究表明:当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当车流密度![]() 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)![]() 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·石家庄一模)祖暅是南北朝时期的伟大数学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖去一个圆锥所得的几何体,图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )
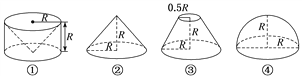
A. ①② B. ①③
C. ②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从含有两件正品a1,a2和一件次品b1的3件产品中每次任取1件,
每次取出后不放回,连续取两次.
(1)求取出的两件产品中恰有一件次品的概率;
(2)如果将“每次取出后不放回”这一条件换成“每次取出后放回”,则取出的两件产品中恰有一件次品的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱锥![]() 中,
中,![]() ,
,![]() ,E为PC的中点,
,E为PC的中点,![]() ,
,![]()

(1)求证:![]()
(2)若![]() 与面ABCD所成角为
与面ABCD所成角为![]() ,P在面ABCD射影为O,问是否在BC上存在一点F,使面
,P在面ABCD射影为O,问是否在BC上存在一点F,使面![]() 与面PAB所成的角为
与面PAB所成的角为![]() ,若存在,试求点F的位置,不存在,请说明理由.
,若存在,试求点F的位置,不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com