
分析 (1)设C(m,n),求得向量BC,DC的坐标,再由向量垂直的条件,解方程即可得到C的坐标;
(2)直线OD的方程为y=-4x,设M(x,-4x),求出向量MA,MB的坐标,再由数量积的坐标表示,结合二次函数的最值求法,即可得到向量OM的坐标.
解答 (1)解:若四边形ABCD为矩形,则$\overrightarrow{BC}⊥\overrightarrow{DC}$,$\overrightarrow{BC}⊥\overrightarrow{AB}$,
设C(m,n),则$\overrightarrow{BC}$=(m-3,n-2),$\overrightarrow{DC}$=(m+1,n-4),
即有$\overrightarrow{BC}$$•\overrightarrow{DC}$=(m-3)•(m+1)+(n-2)(n-4)=0,$\overrightarrow{BC}$$•\overrightarrow{AB}$=m-3+n-2=0,
解得,m=3,n=2(舍去),或m=0,n=5.
即有C(0,5);
(2)解:直线OD的方程为y=-4x,设M(x,-4x),
则$\overrightarrow{MA}$=(2-x,1+4x),$\overrightarrow{MB}$=(3-x,2+4x),$\overrightarrow{MA}•\overrightarrow{MB}$=(2-x)(3-x)+(1+4x)(2+4x)=17x2+7x+8
=17(x+$\frac{7}{34}$)2+$\frac{495}{68}$,
当x=-$\frac{7}{34}$时,$\overrightarrow{MA}$$•\overrightarrow{MB}$取最小值.$\overrightarrow{OM}$的坐标为(-$\frac{7}{34}$,$\frac{14}{17}$).
点评 本题考查向量垂直的条件:数量积为0,同时考查向量的数量积的坐标表示和二次函数的最值求法,属于中档题


科目:高中数学 来源:2016-2017学年云南大理州南涧县民族中学高二文9月月考数学试卷(解析版) 题型:选择题
在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若sin A=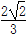 ,a=2,该三角形的面积为
,a=2,该三角形的面积为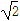 ,则b的值为( )
,则b的值为( )
A.  B.
B. 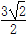 C.2
C.2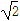 D.2
D.2
查看答案和解析>>
科目:高中数学 来源:2016-2017学年北京昌平临川育人学校等高一上月考一数学试卷(解析版) 题型:选择题
为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为
A.6,4, 1,7 B.7,6,1,4
C.4,6,1,7 D.1,6,4,7
查看答案和解析>>
科目:高中数学 来源:2016-2017学年北京昌平临川育人学校等高一上月考一数学试卷(解析版) 题型:选择题
将集合 表示成列举法,正确的是
表示成列举法,正确的是
A.{2,3} B.{(2,3)} C.{x=2,y=3} D.(2,3)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{25}$ | B. | -$\frac{12}{25}$ | C. | -$\frac{9}{25}$ | D. | $\frac{9}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com