
【题目】如图,已知四棱锥P﹣ABCD中,底面ABCD是棱长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC中点,若H为PD上的动点,EH与平面PAD所成最大角的正切值为 ![]() .
. 
(1)当EH与平面PAD所成角的正切值为 ![]() 时,求证:EH∥平面PAB;
时,求证:EH∥平面PAB;
(2)在(1)的条件下,求二面角A﹣PB﹣C的余弦值.
【答案】
(1)证明:连接AC,由题设知△ABC为正三角形,所以AE⊥BC,
又BC∥AD,因此AE⊥AD;
∵PA⊥平面ABCD,AE平面ABCD,
∴PA⊥AE
而PA平面PAD,AD平面PAD,且PA∩AD=A,
所以AE⊥平面PAD,
则∠EHA为EH与平面PAD所成的角.
在Rt△EAH中,AE= ![]()
所以当AH最短时,∠EHA最大;
即当AH⊥PD时,∠EHA最大;
此时tan∠EHA= ![]() =
= ![]() =
= ![]() ,
,
因此AH= ![]() ,
,
又AD=2,∴∠ADH={45°}∴PA=2
∴H为PD的中点,
取PA的中点M,连接HM,MB,则HM= ![]() 且HM∥AD,DB=
且HM∥AD,DB= ![]() AD且DB∥AD,
AD且DB∥AD,
∴HM∥DB且HM=DB
∴四边形DHMB为平行四边形
∴EH∥BM,
又BM平面PAB
∴EH∥平面PAB
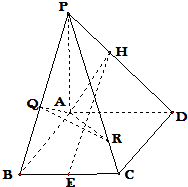
(2)解:∵PA⊥面ABCD,PA平面PAB,
∴平面PAB⊥平面ABCD,
∵PB面PAB∴CM⊥PB,
∴PB⊥面CQM,∴ ![]() ,
,
∴△ABC为正三角形,∴点M为AB的中点,
∴ ![]() ,∴
,∴ ![]() ,
,
∴ 
【解析】(1)首先要证明AE⊥平面PAD,则∠EHA为EH与平面PAD所成的角;所以当AH最短时,∠EHA最大;即当AH⊥PD时,∠EHA最大;接着利用构造平行四边形法判定线面平行即可;(2)利用已知条件证明平面PAB⊥平面ABCD,PB⊥面CQM,所求二面角转化到Rt△CQM中即可;
【考点精析】利用直线与平面平行的判定对题目进行判断即可得到答案,需要熟知平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足S= ![]() (a2+b2﹣c2).
(a2+b2﹣c2).
(1)求角C的大小;
(2)求sinA+sinB的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若x,y∈[﹣1,1],x+y≠0有(x+y)[f(x)+f(y)]>0.
(1)判断f(x)的单调性,并加以证明;
(2)解不等式 ![]() ;
;
(3)若f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立.求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点P(m,n)的直线l与直线l0:x+2y+4=0垂直. (Ⅰ)若 ![]() ,且点P在函数
,且点P在函数 ![]() 的图像上,求直线l的一般式方程;
的图像上,求直线l的一般式方程;
(Ⅱ)若点P(m,n)在直线l0上,判断直线mx+(n﹣1)y+n+5=0是否经过定点?若是,求出该定点的坐标;否则,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对定义域内的任意
对定义域内的任意![]() ,当
,当![]() 时,总有
时,总有![]() ,则称函数
,则称函数![]() 为单调函数,例如函数
为单调函数,例如函数![]() 是单纯函数,但函数
是单纯函数,但函数![]() 不是单纯函数,下列命题:
不是单纯函数,下列命题:
①函数![]() 是单纯函数;
是单纯函数;
②当![]() 时,函数
时,函数![]() 在
在![]() 是单纯函数;
是单纯函数;
③若函数![]() 为其定义域内的单纯函数,
为其定义域内的单纯函数, ![]() ,则
,则![]()
④若函数![]() 是单纯函数且在其定义域内可导,则在其定义域内一定存在
是单纯函数且在其定义域内可导,则在其定义域内一定存在![]() 使其导数
使其导数![]() ,其中正确的命题为__________.(填上所有正确的命题序号)
,其中正确的命题为__________.(填上所有正确的命题序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张先生知道清晨从甲地到乙地有好、中、差三个班次的客车.但不知道具体谁先谁后.他打算:第一辆看后一定不坐,若第二辆比第一辆舒服,则乘第二辆;否则坐第三辆.问张先生坐到好车的概率和坐到差车的概率分别是( )
A.![]() 、
、 ![]()
B.![]() 、
、 ![]()
C.![]() 、
、 ![]()
D.![]() 、
、 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出![]() 盒该产品获利润
盒该产品获利润![]() 元;未售出的产品,每盒亏损
元;未售出的产品,每盒亏损![]() 元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了
元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了![]() 盒该产品,以
盒该产品,以![]() (单位:盒,
(单位:盒, ![]() )表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.
)表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.
(1)根据直方图估计这个开学季内市场需求量![]() 的中位数;
的中位数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润不少于![]() 元的概率.
元的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC,若存在△A1B1C1 , 满足 ![]() =
= ![]() =
= ![]() =1,则称△A1B1C1是△ABC的一个“友好”三角形.在满足下述条件的三角形中,存在“友好”三角形的是:(请写出符合要求的条件的序号) ①A=90°,B=60°,C=30°;②A=75°,B=60°,C=45°;③A=75°,B=75°,C=30°;④A=75°,B=65°,C=45°.
=1,则称△A1B1C1是△ABC的一个“友好”三角形.在满足下述条件的三角形中,存在“友好”三角形的是:(请写出符合要求的条件的序号) ①A=90°,B=60°,C=30°;②A=75°,B=60°,C=45°;③A=75°,B=75°,C=30°;④A=75°,B=65°,C=45°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com