
【题目】已知函数f(x)=ax﹣lnx﹣1.
(1)若函数f(x)在区间[1,+∞)上递增,求实数a的取值范围;
(2)求证: ![]() .
.
【答案】
(1)解:函数f(x)的定义域为(0,+∞).
由题意可得 ![]() 在区间[1,+∞)上恒成立,
在区间[1,+∞)上恒成立,
所以a≥( ![]() )max,又y=
)max,又y= ![]() 在区间[1,+∞)上递减,
在区间[1,+∞)上递减,
所以( ![]() )max=1,
)max=1,
即实数a的取值范围为[1,+∞)
(2)证明:取a=1,由(1)有f(x)在区间[1,+∞)上递增,
所以,当x>1时,f(x)>f(1)=0即lnx<x﹣1,
因为 ![]() ,
,
所以 ![]() ,即
,即 ![]() ,
,
所以: ![]() ,
, ![]() ,
,
ln ![]() <
< ![]() ,…,
,…, ![]() ,ln
,ln ![]() <
< ![]() ,
,
所以: ![]() ,
,
ln2﹣ln1+ln3﹣ln2+…+ln(n+1)﹣lnn+ln(n+2)﹣ln(n+1)<1+ ![]() +
+ ![]() +…+
+…+ ![]() ,
,
即 ![]() ,得证
,得证
【解析】(1)由题意可得 ![]() 在区间[1,+∞)上恒成立,所以a≥(
在区间[1,+∞)上恒成立,所以a≥( ![]() )max,由单调性可得最大值,即可得到a的范围;(2)取a=1,由(1)有f(x)在区间[1,+∞)上递增,可得当x>1时,f(x)>f(1)=0即lnx<x﹣1,因为
)max,由单调性可得最大值,即可得到a的范围;(2)取a=1,由(1)有f(x)在区间[1,+∞)上递增,可得当x>1时,f(x)>f(1)=0即lnx<x﹣1,因为 ![]() ,所以
,所以 ![]() ,即
,即 ![]() ,运用累加法,以及对数的运算性质即可得证.
,运用累加法,以及对数的运算性质即可得证.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0)满足条件:f(x﹣1)=f(3﹣x)且方程f(x)=2x有两个相等实数根 (Ⅰ)求f(x)的解析式;
(Ⅱ)是否存在实数m,n(m<n),使f(x)的定义域和值域分别为[m,n]和[4m,4n],如果存在,求出符合条件的所有m,n的值,如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是ρ=4sinθ,直线l的参数方程是 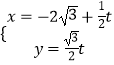 (t为参数).
(t为参数).
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x焦点为F,点D为其准线与x轴的交点,过点F的直线l与抛物线相交于A,B两点,则△DAB的面积S的取值范围为( )
A.[5,+∞)
B.[2,+∞)
C.[4,+∞)
D.[2,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,并制成下面的2×2列联表:
及格 | 不及格 | 合计 | |
很少使用手机 | 20 | 6 | 26 |
经常使用手机 | 10 | 14 | 24 |
合计 | 30 | 20 | 50 |
(1)判断是否有97.5%的把握认为经常使用手机对学习成绩有影响?
(2)从这50人中,选取一名很少使用手机的同学记为甲和一名经常使用手机的同学记为乙,解一道数学题,甲、乙独立解出此题的概率分别为P1 , P2 , 且P2=0.5,若|P1﹣P2|≥0.4,则此二人适合结为学习上互帮互助的“学习师徒”,记X为两人中解出此题的人数,若X的数学期望E(X)=1.4,问两人是否适合结为“学习师徒”? 参考公式及数据: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥K0) | 0.10 | 0.05 | 0.025 | 0.010 |
K0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满分100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
分组 | 频数 | 频率 |
[50,60) | 5 | 0.05 |
[60,70) | a | 0.20 |
[70,80) | 35 | b |
[80,90) | 25 | 0.25 |
[90,100) | 15 | 0.15 |
合计 | 100 | 1.00 |
(I)求a,b的值及随机抽取一考生恰为优秀生的概率;
(Ⅱ)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在[90,100]的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的发展,微信越来越成为人们交流的一种方式.某机构对使用微信交流的态度进行调查,随机调查了 50 人,他们年龄的频数分布及对使用微信交流赞成人数如表.
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(I)由以上统计数据填写下面 2×2 列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若对年龄在[55,65),[65,75)的被调查人中随机抽取两人进行追踪调查,记选中的4人中赞成使用微信交流的人数为X,求随机变量X的分布列和数学期望
参考公式:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
参考数据:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的图象与g(x)=logax(a>0,且a≠1)的图象关于x轴对称,且g(x)的图象过点(9,2).
(1)求函数f(x)的解析式;
(2)若f(3x1)>f(x+5)成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
①y与x负相关且 ![]() =2.347x-6.423;②y与x负相关且
=2.347x-6.423;②y与x负相关且 ![]() =-3.476x+5.648;
=-3.476x+5.648;
③y与x正相关且 ![]() =5.437x+8.493;④y与x正相关且
=5.437x+8.493;④y与x正相关且 ![]() =-4.326x-4.578.
=-4.326x-4.578.
其中一定不正确的结论的序号是( )
A.①②
B.②③
C.③④
D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com