
【题目】如图1,四边形ABCD中AC⊥BD,CE=2AE=2BE=2DE=2,将四边形ABCD沿着BD折叠,得到图2所示的三棱锥A﹣BCD,其中AB⊥CD. 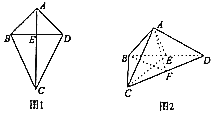
(1)证明:平面ACD⊥平面BAD;
(2)若F为CD中点,求二面角C﹣AB﹣F的余弦值.
【答案】
(1)证明:(1)∵AE⊥BD,且BE=DE,∴△ABD是等腰直角三角形,
∴AB⊥AD,又AB⊥CD,且AD,CD平面ACD,AD∩CD=D,
∴AB⊥平面ACD,
又AB平面BAD,∴平面ACD⊥平面BAD.
(2)解:(2)以E为原点,EC为x轴,ED为y轴,
过E作平面BDC的垂直为z轴,建立空间直角坐标系,
过A作平面BCD的垂线,垂足为G,根据对称性,G点在x轴上,
设AG=h,由题设知:
E(0,0,0),C(2,0,0),B(0,﹣1,0),D(0,1,0),
A( ![]() ,0,h),F(1,
,0,h),F(1, ![]() ,0),
,0), ![]() =(
=( ![]() ,1,h),
,1,h), ![]() =(2,﹣1,0),
=(2,﹣1,0),
∵AB⊥CD,∴ ![]() =2
=2 ![]() ﹣1=0,解得h=
﹣1=0,解得h= ![]() ,
,
∴A( ![]() ).
).
∵ ![]() =(
=( ![]() ),
), ![]() =(1,
=(1, ![]() ,0),
,0),
设平面ABF的法向量 ![]() =(a,b,c),
=(a,b,c),
则  ,
,
令a=9,得 ![]() =(9,﹣6,
=(9,﹣6, ![]() ),
),
∵AD⊥AB,AD⊥AC,
∴2 ![]() =(1,﹣2,
=(1,﹣2, ![]() )是平面ABC的一个法向量,
)是平面ABC的一个法向量,
∴cos< ![]() ,2
,2 ![]() >=
>=  =
= ![]() =
= ![]() ,
,
∵二面角C﹣AB﹣F是锐角,
∴二面角C﹣AB﹣F的余弦值为 ![]() .
.

【解析】(Ⅰ)地出AB⊥AD,AB⊥CD,且AD,由此能证明AB⊥平面ACD,从而得到平面ACD⊥平面BAD.(Ⅱ)以E为原点,EC为x轴,ED为y轴,过E作平面BDC的垂直为z轴,建立空间直角坐标系,利用向量法能求出二面角C﹣AB﹣F的余弦值.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分). 
(1)求图中a的值;
(2)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
(3)将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的分布列与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两地相距500千米,一辆货车从甲地行驶到乙地,规定速度不得超过100千米![]() 小时.已知货车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
小时.已知货车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度![]() (千米
(千米![]() 时)的平方成正比,比例系数为0.01;固定部分为
时)的平方成正比,比例系数为0.01;固定部分为![]() 元(
元(![]() ).
).
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (千米
(千米![]() 时)的函数,并指出这个函数的定义域;
时)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(满分12分)学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如下:
损坏餐椅数 | 未损坏餐椅数 | 总 计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总 计 | 80 | 320 | 400 |
(Ⅰ)求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
(Ⅱ)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
参考公式:![]() ,
,![]()
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() ,直线l:
,直线l:![]() (其中
(其中![]() ).
).
(Ⅰ)求直线l所经过的定点P的坐标;
(Ⅱ)若分别过A,B且斜率为![]() 的两条平行直线截直线l所得线段的长为
的两条平行直线截直线l所得线段的长为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图像如图所示,
的部分图像如图所示,![]() 分别是图像的最低点和最高点,
分别是图像的最低点和最高点,![]()

(1)求函数![]() 的解析式;
的解析式;
(2)将函数![]() 的图像向左平移
的图像向左平移![]() 个单位长度,再把所得图像上各点横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位长度,再把所得图像上各点横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图像,求函数
的图像,求函数![]() 的单调递增区间.
的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数f(x)对任意的实数m,n都有:f(m+n)=f(m)+f(n)-1,
且当x>0时,有f(x)>1.
(1)求f(0).
(2)求证:f(x)在R上为增函数.
(3)若f(1)=2,且关于x的不等式f(ax-2)+f(x-x2)<3对任意的x∈[1,+∞)恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com