
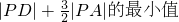 .
.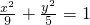 ;
;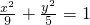 内,连接PD,过P点作PN⊥l(l为右准线)于N点,
内,连接PD,过P点作PN⊥l(l为右准线)于N点, ,即x=
,即x= .
.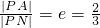 ,?
,? |PA|=|PN|.…(8分)
|PA|=|PN|.…(8分) |PA|=|PD|+|PN|≥|DQ|+|QG|=|DG|=
|PA|=|PD|+|PN|≥|DQ|+|QG|=|DG|= -1=
-1=
 |PA|的最小值为
|PA|的最小值为 .…(13分)
.…(13分)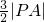 等于点P到右准线的距离|PN|,再结合平面几何垂线段最短的原理,进而推断出
等于点P到右准线的距离|PN|,再结合平面几何垂线段最短的原理,进而推断出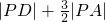 最小值为点D到右准线的距离,不难求得此时的距离最小值.
最小值为点D到右准线的距离,不难求得此时的距离最小值.

科目:高中数学 来源: 题型:
| 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,0)的⊙C的切线方程;
,0)的⊙C的切线方程;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com