
分析 画出三棱锥的侧面展开图,通过截面△DEF过D且平行于AB,求解等腰三角形的斜边的长度即可.
解答 解:三棱锥的展开图如图:三棱锥沿SC侧面展开,各侧面的顶角为30°,展开图顶角为90°,
D为侧棱SC的中点,截面△DEF过D且平行于AB,可得DD′∥AB,
DD′=DE+EF+FD′是截面△DEF周长的最小值.
SC═$\frac{\frac{1}{2}AC}{cos75°}$=$\frac{a}{2(\frac{\sqrt{6}-\sqrt{2}}{2})}$=$\frac{\sqrt{6}+\sqrt{2}}{4}a$.
SD=$\frac{\sqrt{6}+\sqrt{2}}{8}a$,
截得的三棱锥S-DEF的侧面积为:S△SDD′=$\frac{1}{2}$SD2=$\frac{1}{2}$×$(\frac{\sqrt{6}+\sqrt{2}}{8})^{2}{a}^{2}$=$\frac{2+\sqrt{3}}{32}{a}^{2}$.
故答案为:$\frac{2+\sqrt{3}}{32}{a}^{2}$
点评 本题考查三棱锥的结构特征,直线与平面平行的性质定理的应用,侧面展开图的应用,考查计算能力.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
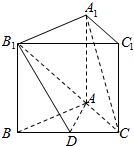 已知正三棱柱ABC-A1B1C1中,BC=1,D是棱BC上的动点.
已知正三棱柱ABC-A1B1C1中,BC=1,D是棱BC上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,1] | B. | [0,5] | C. | [-4,1]∪[0,5] | D. | [-2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
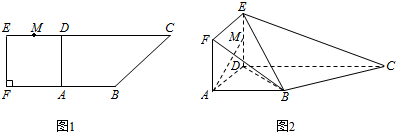
 在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )
在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,∠ABC=$\frac{π}{2}$,∠BAC=∠CAD=$\frac{π}{3}$,PA⊥平面ABCD,E为PD的中点,PA=2AB=2,CD=2$\sqrt{3}$.
在四棱锥P-ABCD中,∠ABC=$\frac{π}{2}$,∠BAC=∠CAD=$\frac{π}{3}$,PA⊥平面ABCD,E为PD的中点,PA=2AB=2,CD=2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com