
°æƒø°ø‘⁄°∞¥¥Œƒ¥¥Œ¿°±ªÓ∂Ø÷–£¨ƒ≥ª˙ππŒ™¡ÀΩ‚“ª–°«¯≥…ƒÍæ”√Ò°∞Œ¸—ÔΖ‘±°± «∑Ò”–πÿ.¥”∏√–°«¯÷–Àʪ˙≥È»°200Œª≥…ƒÍæ”√Ò£¨µ√µΩœ¬±þ¡–¡™±Ì:“—÷™‘⁄»´≤ø200»À÷–Àʪ˙≥È»°1»À£¨≥ȵΩ≤ªŒ¸—õƒ∏≈¬ Œ™0.75.
Œ¸—à | ≤ªŒ¸—à | ∫œº∆ | |
ƒ– | 40 | ||
Ů | 90 | ||
∫œº∆ | 200 |
(1)≤π≥‰…œ√ʵƒ¡–¡™±Ì£¨≤¢≈–∂œ:ƒÐ∑Ò”–99.9%µƒ∞—Œ’»œŒ™°∞Œ¸—ÔΖ‘±°±”–πÿ£ª
(2)”√∑÷≤„≥È—˘µƒ∑Ω∑®¥”Œ¸—Ãæ”√Ò÷–—°5»À≥ˆ¿¥£¨»ª∫Û‘Ÿ¥”÷–≥È2»À≥ˆ¿¥£¨∏¯–°«¯æ”√ÒÃ∏Ã∏Œ¸—õƒŒ£∫¶–‘£¨«Û«°∫√≥ÈµΩ°∞“ªƒ–“ª≈Æ°±µƒ∏≈¬ .
≤Œøºπ´ Ω: 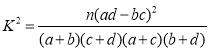 .
.
≤Œøº ˝æð:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
°æ¥∞∏°ø£®1£©¡–¡™±ÌœÍº˚Ω‚Œˆ£¨”–99.9%µƒ∞—Œ’»œŒ™°∞Œ¸—ÔΖ‘±°±”–πÿ£ª£®2£©![]()
°æΩ‚Œˆ°ø
£®1£©”…Ãıº˛ÃÓ–¥¡–¡™±Ì£¨»ª∫Ûº∆À„![]() ∫Õ10.828±»Ωœ¥Û–°£¨◊ˆ≥ˆ≈–∂œ£ª
∫Õ10.828±»Ωœ¥Û–°£¨◊ˆ≥ˆ≈–∂œ£ª
£®2£©∑÷≤„≥È—˘ø…÷™£¨ƒ–…˙÷–—°4»À£¨≈Æ…˙÷–—°1»À£¨»ª∫Û“ª“ª¡–æŸ≥ˆÀ˘”–µƒª˘±æ ¬º˛∫Õ¬˙◊„Ãıº˛µƒª˘±æ ¬º˛µƒ∏ˆ ˝£¨«Û∏≈¬ .
£®1£©”…Ãıº˛ø…÷™![]() »À£¨
»À£¨
À˘“‘ƒ–…˙÷–≤ªŒ¸—õƒ»À ˝Œ™![]() »À£¨
»À£¨
≈Æ…˙÷–Œ¸—ûÀ ˝Œ™![]() »À£¨
»À£¨
¡–¡™±Ì»Áœ¬£∫
Œ¸—à | ≤ªŒ¸—à | ∫œº∆ | |
ƒ– | 40 | 60 | 100 |
Ů | 10 | 90 | 100 |
∫œº∆ | 50 | 150 | 200 |
 £¨
£¨
![]() ”–99.9%µƒ∞—Œ’»œŒ™°∞Œ¸—ÔΖ‘±°±”–πÿ£ª
”–99.9%µƒ∞—Œ’»œŒ™°∞Œ¸—ÔΖ‘±°±”–πÿ£ª
£®2£©”…∑÷≤„≥È—˘ø…÷™£¨ƒ–…˙÷–—°4»À£¨≈Æ…˙÷–—°1»À£¨
ƒ–…˙…ËŒ™![]() £¨≈Æ…˙…ËŒ™
£¨≈Æ…˙…ËŒ™![]() £¨
£¨
‘Ú»Œ—°2»Àµƒª˘±æ ¬º˛Œ™![]() £¨
£¨![]() £¨
£¨
![]() ,π≤10∏ˆª˘±æ ¬º˛£¨
,π≤10∏ˆª˘±æ ¬º˛£¨
∆‰÷–«°∫√≥ÈµΩ°∞“ªƒ–“ª≈Æ°±µƒπ≤”–![]() π≤4∏ˆª˘±æ ¬º˛£¨
π≤4∏ˆª˘±æ ¬º˛£¨
‘Ú«°∫√≥ÈµΩ°∞“ªƒ–“ª≈Æ°±µƒ∏≈¬ «![]() .
.


 100∑÷¥≥πÿ∆⁄ƒ©≥¥Üµ¡–¥∞∏
100∑÷¥≥πÿ∆⁄ƒ©≥¥Üµ¡–¥∞∏ √˚–£¡™√ÀøÏ¿÷øŒÃ√œµ¡–¥∞∏
√˚–£¡™√ÀøÏ¿÷øŒÃ√œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë ˝¡–![]()
![]() «π´≤Ó≤ªŒ™¡„µ»≤Ó ˝¡–£¨¬˙◊„
«π´≤Ó≤ªŒ™¡„µ»≤Ó ˝¡–£¨¬˙◊„![]() £ª ˝¡–
£ª ˝¡–![]()
![]() µƒ«∞
µƒ«∞![]() œÓ∫ÕŒ™
œÓ∫ÕŒ™![]() £¨«“¬˙◊„
£¨«“¬˙◊„![]() .
.
£®1£©«Û ˝¡–![]() °¢
°¢![]() µƒÕ®œÓπ´ Ω£ª
µƒÕ®œÓπ´ Ω£ª
£®2£©‘⁄![]() ∫Õ
∫Õ![]() ÷ƺ‰≤»Î1∏ˆ ˝
÷ƺ‰≤»Î1∏ˆ ˝![]() £¨ π
£¨ π![]() ≥…µ»≤Ó ˝¡–£ª‘⁄
≥…µ»≤Ó ˝¡–£ª‘⁄![]() ∫Õ
∫Õ![]() ÷ƺ‰≤»Î2∏ˆ ˝
÷ƺ‰≤»Î2∏ˆ ˝![]() £¨ π
£¨ π![]() ≥…µ»≤Ó ˝¡–£ª°≠°≠£ª‘⁄
≥…µ»≤Ó ˝¡–£ª°≠°≠£ª‘⁄![]() ∫Õ
∫Õ![]() ÷ƺ‰≤»Î
÷ƺ‰≤»Î![]() ∏ˆ ˝
∏ˆ ˝![]() £¨ π
£¨ π![]() ≥…µ»≤Ó ˝¡–£¨
≥…µ»≤Ó ˝¡–£¨
£®i£©«Û![]() £ª
£ª
£®ii£© «∑ҥʑ⁄’˝’˚ ˝![]() £¨ π
£¨ π![]() ≥…¡¢£ø»Ù¥Ê‘⁄£¨«Û≥ˆÀ˘”–µƒ’˝’˚ ˝∂‘
≥…¡¢£ø»Ù¥Ê‘⁄£¨«Û≥ˆÀ˘”–µƒ’˝’˚ ˝∂‘![]() £ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £Æ
£Æ
(1)»Ù![]() £¨«Û∫Ø ˝
£¨«Û∫Ø ˝![]() µƒÀ˘”–¡„µ„£ª
µƒÀ˘”–¡„µ„£ª
(2)»Ù![]() £¨÷§√˜∫Ø ˝
£¨÷§√˜∫Ø ˝![]() ≤ª¥Ê‘⁄º´÷µ£Æ
≤ª¥Ê‘⁄º´÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÕ÷‘≤![]() µƒ◊Û°¢”“∂•µ„∑÷±Œ™
µƒ◊Û°¢”“∂•µ„∑÷±Œ™![]() £¨…œ°¢œ¬∂•µ„∑÷±Œ™
£¨…œ°¢œ¬∂•µ„∑÷±Œ™![]() £¨◊Û°¢”“Ωπµ„∑÷±Œ™
£¨◊Û°¢”“Ωπµ„∑÷±Œ™![]() £¨
£¨![]() £¨¿Î–ƒ¬ Œ™
£¨¿Î–ƒ¬ Œ™![]() .
.
£®1£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©π˝”“Ωπµ„![]() µƒ÷±œþ
µƒ÷±œþ![]() ”ÎÕ÷‘≤
”ÎÕ÷‘≤![]() œýΩª”⁄
œýΩª”⁄![]() ¡Ωµ„£¨ ‘ÃΩæø‘⁄
¡Ωµ„£¨ ‘ÃΩæø‘⁄![]() ÷·…œ «∑ҥʑ⁄∂®µ„
÷·…œ «∑ҥʑ⁄∂®µ„![]() £¨ πµ√ø…
£¨ πµ√ø…![]() Œ™∂®÷µ£ø»Ù¥Ê‘⁄£¨«Û≥ˆµ„
Œ™∂®÷µ£ø»Ù¥Ê‘⁄£¨«Û≥ˆµ„![]() µƒ◊¯±Í£¨»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£ø
µƒ◊¯±Í£¨»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨Àƒ¿‚◊∂![]() µƒµ◊√Ê «’˝∑Ω–Œ£¨
µƒµ◊√Ê «’˝∑Ω–Œ£¨![]() ∆Ω√Ê
∆Ω√Ê![]() £¨
£¨![]() .
.
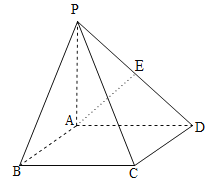
£®1£©÷§√˜£∫![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®2£©»Ù![]() £¨«Û∂˛√ÊΩ«
£¨«Û∂˛√ÊΩ«![]() µƒ”ýœ“÷µ.
µƒ”ýœ“÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £¨£®x£æ0£©£Æ
£¨£®x£æ0£©£Æ
£®1£©µ±0£ºa£ºb£¨«“f£®a£©£Ωf£®b£© ±£¨«Û÷§£∫ab£æ1£ª
£®2£© «∑ҥʑ⁄ µ ˝a£¨b£®a£ºb£©£¨ πµ√∫Ø ˝y£Ωf£®x£©µƒ∂®“”ڰ¢÷µ”Ú∂º «[a£¨b]£¨»Ù¥Ê‘⁄£¨‘Ú«Û≥ˆa£¨bµƒ÷µ£¨»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
£®3£©»Ù¥Ê‘⁄ µ ˝a£¨b£®a£ºb£©£¨ πµ√∫Ø ˝y£Ωf£®x£©µƒ∂®“”ڌ™[a£¨b] ±£¨÷µ”ÚŒ™[ma£¨mb]£®m°Ÿ0£©£¨«Ûmµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥—ß–£≥…¡¢¡À ˝—ß°¢”¢”Ô°¢“Ù¿÷3∏ˆøŒÕ‚–À»§–°◊È£¨3∏ˆ–°◊È∑÷±”–39°¢32°¢33∏ˆ≥…‘±£¨“ª–©≥…‘±≤Œº”¡À≤ª÷π“ª∏ˆ–°◊È£¨æþëÈøˆ»ÁÕºÀ˘ æ£Æ
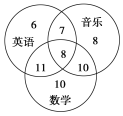
œ÷Àʪ˙—°»°“ª∏ˆ≥…‘±£¨À˚ Ù”⁄÷¡…Ÿ2∏ˆ–°◊ȵƒ∏≈¬ «________£¨À˚ Ù”⁄≤ª≥¨π˝2∏ˆ–°◊ȵƒ∏≈¬ «________£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™≈◊ŒÔœþE£∫![]() µƒΩπµ„Œ™F£¨π˝Fµƒ÷±œþl”ÎEΩª”⁄A£¨B¡Ωµ„£¨”Îx÷·Ωª”⁄µ„
µƒΩπµ„Œ™F£¨π˝Fµƒ÷±œþl”ÎEΩª”⁄A£¨B¡Ωµ„£¨”Îx÷·Ωª”⁄µ„![]() .»ÙAŒ™œþ∂Œ
.»ÙAŒ™œþ∂Œ![]() µƒ÷–µ„£¨‘Ú
µƒ÷–µ„£¨‘Ú![]() £® £©
£® £©
A.9B.12C.18D.72
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™iŒ™–È ˝µ•Œª£¨aŒ™ µ ˝£¨∏¥ ˝z=£®1©Å2i£©£®a+i£©‘⁄∏¥∆Ω√ʃ⁄∂‘”¶µƒµ„Œ™M£¨‘Ú![]() °∞°± «°∞µ„M‘⁄µ⁄ÀƒœÛœÞ°±µƒ£® £©
°∞°± «°∞µ„M‘⁄µ⁄ÀƒœÛœÞ°±µƒ£® £©
A.≥‰∑÷∂¯≤ª±ÿ“™Ãıº˛
B.±ÿ“™∂¯≤ª≥‰∑÷Ãıº˛
C.≥‰“™Ãıº˛
D.º»≤ª≥‰∑÷“≤≤ª±ÿ“™Ãıº˛
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com