
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
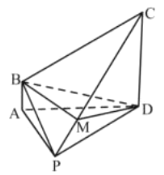
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 平面
平面![]() ,求此时三棱椎
,求此时三棱椎![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用正弦定理和三角形的内角和定理证得![]() ,结合
,结合![]() ,利用线面垂直的判定定理证得
,利用线面垂直的判定定理证得![]() 平面
平面![]() ,再由面面垂直的判定定理即可证明;
,再由面面垂直的判定定理即可证明;
(2)如图所示,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,可证明
,可证明![]() ~
~![]() ,
,![]() ,由
,由![]() ,作
,作![]() 于点
于点![]() ,可证
,可证![]() 平面
平面![]() ,代入题中的数据进行计算,即可求出
,代入题中的数据进行计算,即可求出![]() 的体积.
的体积.
(1)证明:因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
由正弦定理可得,![]() ,解得
,解得![]() ,
,
所以![]() ,
,![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)如图:连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
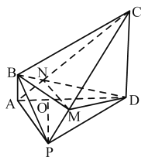
因为直线![]() 平面
平面![]() ,过
,过![]() 的平面
的平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,
,
由线面平行的性质定理可得,![]() ,
,
在梯形![]() 中,因为
中,因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ~
~![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]()
![]()
![]() ,
,
∴![]() ,即
,即![]() ,
,
作![]() 于点
于点![]() ,因为
,因为![]() 平面
平面![]() ,
,
所以![]() ,因为
,因为![]() ,
,
所以![]() 平面
平面![]() ,
,
在![]() 中,由(1)知,
中,由(1)知,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() 即为所求.
即为所求.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】某公司为抓住经济发展的契机,调查了解了近几年广告投入对销售收益的影响,在若干销售地区分别投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
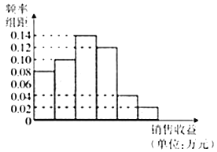
(1)根据频率分布直方图计算图中各小长方形的宽度;并估计该公司分别投入4万元广告费用之后,对应地区销售收益的平均值(以各组的区间中点值代表该组的取值);
(2)该公司按照类似的研究方法,测得另外一些数据,并整理得到如表:
广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
销售收益y(单位:万元) | 2 | 3 | 2 | 7 |
由表中的数据显示,x与y之间存在着线性相关关系,请将(1)的结果填入空白栏,根据表格中数据求出y关于x的回归真线方程![]() ,并估计该公司下一年投入广告费多少万元时,可使得销售收益达到8万元?
,并估计该公司下一年投入广告费多少万元时,可使得销售收益达到8万元?
参考公式:最小二乘法估计分别为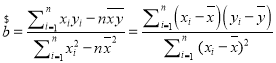 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解户籍、性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为200的调查样本,其中城镇户籍与农村户籍各100人;男性120人,女性80人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图,如图所示,其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
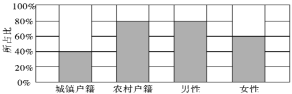
A. 是否倾向选择生育二胎与户籍有关
B. 是否倾向选择生育二胎与性别有关
C. 倾向选择生育二胎的人群中,男性人数与女性人数相同
D. 倾向选择不生育二胎的人群中,农村户籍人数少于城镇户籍人数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 与
与![]() 满足的关系;
满足的关系;
(2)当![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(3)当![]() 时,对任意的
时,对任意的![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某摄影协会在2019年10月举办了主题“庆祖国70华诞——我们都是追梦人”摄影图片展.通过平常人的镜头,记录了国强民富的幸福生活,向祖国母亲70岁的生日献了一份厚礼.摄影协会收到了来自社会各界的大量作品,从众多照片中选取100张照片展出,其参赛者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:
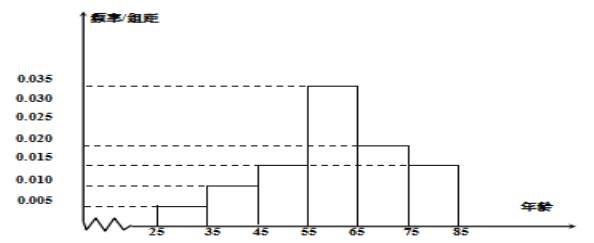
(1)求这100位作者年龄的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(2)由频率分布直方图可以认为,作者年龄X服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
附:![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
(ii)摄影协会从年龄在![]() 和
和![]() 的作者中,按照分层抽样的方法,抽出了7人参加“讲述图片背后的故事”座谈会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间
的作者中,按照分层抽样的方法,抽出了7人参加“讲述图片背后的故事”座谈会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间![]() 的人数是Y,求变量Y的分布列和数学期望.
的人数是Y,求变量Y的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线上任意两点![]()
![]() 处的切线交于点
处的切线交于点![]() ,称
,称![]() 为“阿基米德三角形”.当线段
为“阿基米德三角形”.当线段![]() 经过抛物线焦点
经过抛物线焦点![]() 时,
时,![]() 具有以下特征:①
具有以下特征:①![]() 点必在抛物线的准线上;②
点必在抛物线的准线上;②![]() 为直角三角形,且
为直角三角形,且![]() ;③
;③![]() .若经过抛物线
.若经过抛物线![]() 焦点的一条弦为
焦点的一条弦为![]() ,阿基米德三角形为
,阿基米德三角形为![]() ,且点
,且点![]() 的纵坐标为4,则直线
的纵坐标为4,则直线![]() 的方程为( )
的方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】疫情期间,一同学通过网络平台听网课,在家坚持学习.某天上午安排了四节网课,分别是数学,语文,政治,地理,下午安排了三节,分别是英语,历史,体育.现在,他准备在上午下午的课程中各任选一节进行打卡,则选中的两节课中至少有一节文综学科(政治、历史、地理)课程的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com