练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知，其中ω＞0．设函数，且函数f（x）的周期为π．
    （I）求ω的值；
    （Ⅱ）在△ABC中，a，b，c分别是角A，B，C的对边，且a，b，c成等差：当f（B）=1'时，判断△ABC的形状．
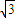    【答案】分析：（I）根据向量积得出f（x）=cos2ωx+sin2ωx进而化简成f（x）=2sin（2ωx+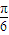），然后根据周期公式得出答案．
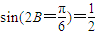    （II） 首先根据条件求出，进而由角的范围求出B的度数，再由等差数列的性质得出2b=a+c，从而利用余弦定理求出角B的度数进而判断三角形的形状．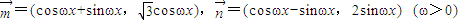
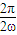    解答：解：
    （I）∵
    ∵函数f（x）的周期为π∴T==π∴ω=1
    （Ⅱ）在△ABC中∴
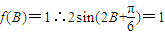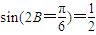
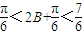    又∵0＜B＜π∴π
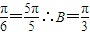    ∵2B+∵a，b，c成等差∴2b=a+c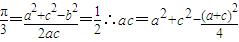
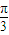    ∴cosB=cos
    化简得：a=c又∵B=∴△ABC为正三角形
    点评：本题考查了三角函数周期性的求法以及利用余弦定理判断三角形的形状，解题过程要特别注意角的范围，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2009•河西区二模）已知定义在正实数集上的函数f（x）=
    3x22
    +ax，g（x）=4a2lnx+b，其中a＞0，设两曲线x=f（x）与f=g（x）有公共点，且在公共点处的切线相同．
    （I）若a=1，求两曲线y=f（x）与y=g（x）在公共点处的切线方程；
    （Ⅱ）用a表示b，并求b的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

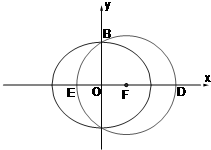    精英家教网如图，已知F（c，0）是椭圆C：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的右焦点；⊙F：（x-c）2+y2=a2与x轴交于D，E两点，其中E是椭圆C的左焦点．
    （1）求椭圆C的离心率；
    （2）设⊙F与y轴的正半轴的交点为B，点A是点D关于y轴的对称点，试判断直线AB与⊙F的位置关系；
    （3）设直线BF与⊙F交于另一点G，若△BGD的面积为4
    		3
    ，求椭圆C的标准方程．

    查看答案和解析>>

    科目：高中数学 来源：2012年全国普通高等学校招生统一考试文科数学（天津卷解析版） 题型：解答题

    已知函数其中a>0.

    （I）求函数f(x)的单调区间；

    （II）若函数f（x）在区间（-2，0）内恰有两个零点，求a的取值范围；

    （III）当a=1时，设函数f（x）在区间[t,t+3]上的最大值为M（t），最小值为m（t）,记g(t)=M(t)-m(t),求函数g(t)在区间[-3，-1]上的最小值。

    【考点定位】本小题主要考查导数的运算，利用导数研究函数的单调性、函数的零点，函数的最值等基础知识.考查函数思想、分类讨论思想.考查综合分析和解决问题的能力.

     

    查看答案和解析>>

    科目：高中数学 来源：四川省绵阳市高中2010届高三二诊（文） 题型：解答题

     

    已知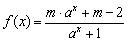（其中a>0且a≠1，m∈R）是定义在R上的奇函数．记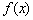的反函数为．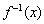

    （1）求实数m的值及；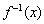

    （2）设数列{an}满足an=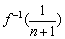（n∈N*），它的前n项和为Sn，求使不等式Sn<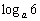成立的n的取值．

     

     

     

     

     

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数其中a<0,且a≠-1．

    （Ⅰ）讨论函数的单调性；

    （Ⅱ）设函数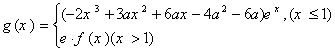（e是自然对数的底数），是否存在a，使在[a,-a]上为减函数？若存在，求a的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案