
【题目】如图,椭圆![]() 经过点
经过点![]() ,离心率
,离心率![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
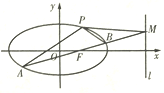
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]()
![]() 是经过右焦点
是经过右焦点![]() 的任一弦(不经过点
的任一弦(不经过点![]() ),设直线
),设直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,记
,记![]() ,
, ![]() ,
, ![]() 的斜率为
的斜率为![]() ,
, ![]() ,
, ![]() .问:是否存在常数
.问:是否存在常数![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx﹣ ![]() (a>0),g(x)=4x+
(a>0),g(x)=4x+ ![]() +
+ ![]() ,且y=f(x+
,且y=f(x+ ![]() )为偶函数.设集合A={x|t﹣1≤x≤t+1}.
)为偶函数.设集合A={x|t﹣1≤x≤t+1}.
(1)若t=﹣ ![]() ,记f(x)在A上的最大值与最小值分别为M,N,求M﹣N;
,记f(x)在A上的最大值与最小值分别为M,N,求M﹣N;
(2)若对任意的实数t,总存在x1 , x2∈A,使得|f(x1)﹣f(x2)|≥g(x)对x∈[0,1]恒成立,试求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,过F作垂直于x轴的直线交抛物线于A,B,两点,△AOB的面积为8,直线l与抛物线C相切于Q点,P是l上一点(不与Q重合). 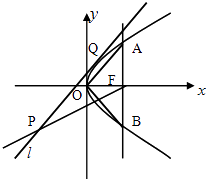
(1)求抛物线C的方程;
(2)若以线段PQ为直径的圆恰好经过F,求|PF|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为2的正方体ABCD﹣A1B1C1D1中,点P是正方体棱上的一点(不包括棱的端点),满足|PB|+|PD1|= ![]() 的点P的个数为;若满足|PB|+|PD1|=m的点P的个数为6,则m的取值范围是 .
的点P的个数为;若满足|PB|+|PD1|=m的点P的个数为6,则m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省![]() 情况图,则下列陈述正确的是( )
情况图,则下列陈述正确的是( )
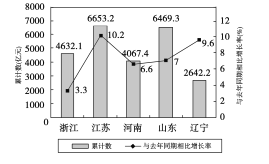
①2017年第一季度 ![]() 总量和增速均居同一位的省只有1个;
总量和增速均居同一位的省只有1个;
②与去年同期相比,2017年第一季度五个省的![]() 总量均实现了增长;
总量均实现了增长;
③去年同期的![]() 总量前三位是江苏、山东、浙江;
总量前三位是江苏、山东、浙江;
④2016年同期浙江的![]() 总量也是第三位.
总量也是第三位.
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() 写出曲线
写出曲线![]() 的极坐标的方程以及曲线
的极坐标的方程以及曲线![]() 的直角坐标方程;
的直角坐标方程;
![]() 若过点
若过点![]() (极坐标)且倾斜角为
(极坐标)且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,弦
两点,弦![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 经过点
经过点![]() ,离心率
,离心率![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
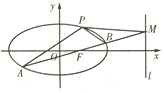
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]()
![]() 是经过右焦点
是经过右焦点![]() 的任一弦(不经过点
的任一弦(不经过点![]() ),设直线
),设直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,记
,记![]() ,
, ![]() ,
, ![]() 的斜率为
的斜率为![]() ,
, ![]() ,
, ![]() .问:是否存在常数
.问:是否存在常数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①一个命题的逆命题为真,它的否命题也一定为真;
②在△ABC中,“∠B=60°”是“∠A,∠B,∠C三个角成等差数列”的充要条件.
③ ![]() 是
是 ![]() 的充要条件;
的充要条件;
④“am2<bm2”是“a<b”的充分必要条件.
以上说法中,判断错误的有 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com