
【题目】已知![]()
(1)求曲线![]() 在点
在点![]() 出的切线方程;
出的切线方程;
(2)设函数![]() ,若不等式
,若不等式![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)求出![]() ,由
,由![]() 的值可得切点坐标,求出
的值可得切点坐标,求出![]() 的值,可得切线斜率,利用点斜式可得曲线
的值,可得切线斜率,利用点斜式可得曲线![]() 在点
在点![]() 处的切线方程;(2)
处的切线方程;(2)![]() ,等价于
,等价于![]() ,
,![]() ,
,![]() ,利用导数研究函数的单调性,可得要满足
,利用导数研究函数的单调性,可得要满足![]() 对
对![]() 恒成立,只需
恒成立,只需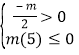 ,从而可得结果.
,从而可得结果.
详解:(1)由题知:![]() ,则
,则![]() ,
,
∴曲线在点![]() 处切线的斜率为
处切线的斜率为![]()
所以,切线方程为![]() ,即
,即![]() .
.
(2)由题知:![]() ,即
,即![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() 解得
解得![]() ,
,
∴![]() 在
在![]() 单增;
单增;![]() 单减,
单减,
又∵![]() 有唯一零点
有唯一零点![]()
所以,可作出函数![]() 的示意图,
的示意图,
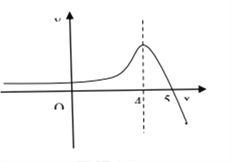
要满足![]() 对
对![]() 恒成立,只需
恒成立,只需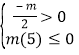 解得
解得![]() .即实数
.即实数![]() 的取值范围是
的取值范围是![]()
法二:令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() , 令
, 令![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 单增,
单增,![]() 单减;
单减;![]() ,故
,故![]() 对
对![]() 恒成立.
恒成立.
∴![]() 在
在![]() 单减,
单减,
又∵![]() 对
对![]() 恒成立,令
恒成立,令![]() 得
得![]()
∴![]() ,无论
,无论![]() 在
在![]() 有无零点,
有无零点,
∴![]() 在
在![]() 上的最小值只可能为
上的最小值只可能为![]() 或
或![]() ,
,
要![]() 恒成立,
恒成立,
∴![]() 且
且![]() ,
,
∴![]() .即实数
.即实数![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】综合题。
(1)设不等式(x﹣a)(x+a﹣2)<0的解集为N, ![]() ,若x∈N是x∈M的必要条件,求a的取值范围.
,若x∈N是x∈M的必要条件,求a的取值范围.
(2)已知命题:“x∈{x|﹣1<x<1},使等式x2﹣x﹣m=0成立”是真命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次抽样调查中测得样本的5个样本点,数值如下表:
| 0.25 | 0.5 | 1 | 2 | 4 |
| 16 | 12 | 5 | 2 | 1 |
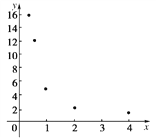
(1)根据散点图判断,![]() 哪一个适宜作为
哪一个适宜作为![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果试建立![]() 与
与![]() 之间的回归方程.(注意
之间的回归方程.(注意![]() 或
或![]() 计算结果保留整数)
计算结果保留整数)
(3)由(2)中所得设z=![]() +
+![]() 且
且![]() ,试求z的最小值。
,试求z的最小值。
参考数据及公式如下:
![]() ,
,![]() ,
,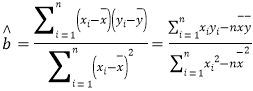
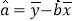
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极小值;
的极小值;
(2)若函数![]() 在
在![]() 有
有![]() 个零点,求实数
个零点,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若函数![]() 在
在![]() 的三个零点分别为
的三个零点分别为![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC-A![]() B
B![]() C
C![]() 中,AB=BC=
中,AB=BC=![]() ,BB
,BB![]() =2,
=2,![]() ABC=90
ABC=90![]() ,E、F分别为AA
,E、F分别为AA![]() 、C
、C![]() B
B![]() 的中点,沿棱柱的表面从E到F两点的最短路径的长度为_______
的中点,沿棱柱的表面从E到F两点的最短路径的长度为_______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ<![]() )的图象与x轴的交点中,相邻两条对称轴之间的距离为
)的图象与x轴的交点中,相邻两条对称轴之间的距离为![]() ,且图象上一个最低点为M
,且图象上一个最低点为M![]() .
.
(1)求ω,φ的值;
(2)求f(x)的图像的对称中心;
(3)当x∈![]() 时,求f(x)的值域.
时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,D是 ![]() 的中点,BD交AC于E. (Ⅰ)求证:DC2=DEDB;
的中点,BD交AC于E. (Ⅰ)求证:DC2=DEDB;
(Ⅱ)若CD=2 ![]() ,O到AC的距离为1,求⊙O的半径r.
,O到AC的距离为1,求⊙O的半径r.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A、B、C三位老师分别教数学、英语、体育、劳技、语文、阅读六门课,每位教两门.已知:
(1)体育老师和数学老师住在一起,
(2)A老师是三位老师中最年轻的,
(3)数学老师经常与C老师下象棋,
(4)英语老师比劳技老师年长,比B老师年轻,
(5)三位老师中最年长的老师比其他两位老师家离学校远.
问:A、B、C三位老师每人各教哪几门课?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com