
【题目】已知圆![]() ,直线
,直线![]() ,
,![]() 为任意实数.
为任意实数.
(1)求证:直线![]() 必与圆
必与圆![]() 相交;
相交;
(2)![]() 为何值时,直线
为何值时,直线![]() 被圆
被圆![]() 截得的弦长
截得的弦长![]() 最短?最短弦长是多少?
最短?最短弦长是多少?
(3)若直线![]() 被圆
被圆![]() 截得的弦
截得的弦![]() 的中点为点
的中点为点![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
科目:高中数学 来源: 题型:
【题目】在明代程大位所著的《算法统宗》中有这样一首歌谣,“放牧人粗心大意,三畜偷偷吃苗青,苗主扣住牛马羊,要求赔偿五斗粮,三畜户主愿赔偿,牛马羊吃得异样.马吃了牛的一半,羊吃了马的一半.”请问各畜赔多少?它的大意是放牧人放牧时粗心大意,牛、马、羊偷吃青苗,青苗主人扣住牛、马、羊向其主人要求赔偿五斗粮食(1斗=10升),三畜的主人同意赔偿,但牛、马、羊吃的青苗量各不相同.马吃的青苗是牛的一半,羊吃的青苗是马的一半.问羊、马、牛的主人应该分别向青苗主人赔偿多少升粮食?( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国家积极推动美丽乡村建设的政策背景下,各地根据当地生态资源打造了众多特色纷呈的乡村旅游胜地.某人意图将自己位于乡村旅游胜地的房子改造成民宿用于出租,在旅游淡季随机选取100天,对当地已有的六间不同价位的民宿进行跟踪,统计其出租率![]() (
(![]() ),设民宿租金为
),设民宿租金为![]() (单位:元/日),得到如图所示的数据散点图.
(单位:元/日),得到如图所示的数据散点图.
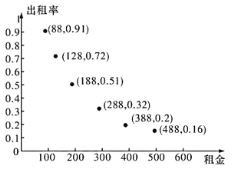
(1)若用“出租率”近似估计旅游淡季民宿每天租出去的概率,求租金为388元的那间民宿在淡季内的三天中至少有2天闲置的概率.
(2)①根据散点图判断,![]() 与
与![]() 哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
②若该地一年中旅游淡季约为280天,在此期间无论民宿是否出租,每天都要付出![]() 的固定成本,若民宿出租,则每天需要再付出
的固定成本,若民宿出租,则每天需要再付出![]() 的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益
的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益![]() 达到最大?
达到最大?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;![]() .
.
参考数据:记![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面四边形ABCD是菱形,对角线AC与BD交于点O,
中,底面四边形ABCD是菱形,对角线AC与BD交于点O,![]() .
.
![]() 求证:平面
求证:平面![]() 平面PBD;
平面PBD;
![]() 若
若![]() ,
,![]() ,
,![]() ,E为线段PA的中点,求二面角
,E为线段PA的中点,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若对任意的正整数![]() ,总存在正整数
,总存在正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ,则称
,则称![]() 是“回归数列”.
是“回归数列”.
(1)①前![]() 项和为
项和为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
②通项公式为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
(2)设![]() 是等差数列,首项
是等差数列,首项![]() ,公差
,公差![]() ,若
,若![]() 是“回归数列”,求
是“回归数列”,求![]() 的值;
的值;
(3)是否对任意的等差数列![]() ,总存在两个“回归数列”
,总存在两个“回归数列”![]() 和
和![]() ,使得
,使得![]() 成立,请给出你的结论,并说明理由.
成立,请给出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年一种新奇水果深受广大消费者的喜爱,一位农户发挥聪明才智,把这种露天种植的新奇水果搬到了大棚里,收到了很好的经济效益.根据资料显示,产出的新奇水果的箱数x(单位:十箱)与成本y(单位:千元)的关系如下:
x | 1 | 3 | 4 | 6 | 7 |
y | 5 | 6.5 | 7 | 7.5 | 8 |
y与x可用回归方程![]() (其中
(其中![]() ,
,![]() 为常数)进行模拟.
为常数)进行模拟.
(1)若该农户产出的该新奇水果的价格为150元/箱,试预测该新奇水果100箱的利润是多少元.(利润=售价-成本)
(2)据统计,10月份的连续16天中该农户每天为甲地可配送的该新奇水果的箱数的频率分布直方图如图,用这16天的情况来估计相应的概率.一个运输户拟购置n辆小货车专门运输该农户为甲地配送的该新奇水果,一辆货车每天只能运营一趟,每辆车每趟最多只能装载40箱该新奇水果,满载发车,否则不发车.若发车,则每辆车每趟可获利500元,若未发车,则每辆车每天平均亏损200元试比较![]() 和
和![]() 时此项业务每天的利润平均值的大小.
时此项业务每天的利润平均值的大小.
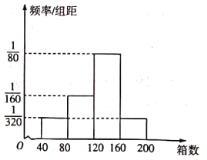
参考数据与公式:设![]() ,则
,则
|
|
|
|
0.54 | 6.8 | 1.53 | 0.45 |
线性回归直线![]() 中,
中, ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com