
【题目】已知正方体![]() 的棱长为
的棱长为![]() ,
,![]() 为
为![]() 的中点,下列说法中正确的是( )
的中点,下列说法中正确的是( )
A.![]() 与
与![]() 所成的角大于
所成的角大于![]()
B.点![]() 到平面
到平面![]() 的距离为
的距离为![]()
C.三棱锥![]() 的外接球的表面积为
的外接球的表面积为![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
【答案】D
【解析】
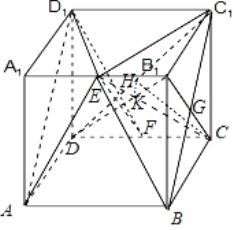
对于A,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 为
为![]() 与
与![]() 所成的角,可求得该角正切值:
所成的角,可求得该角正切值: ![]() ;对于B,
;对于B, ![]() 到平面
到平面![]() 的距离即点
的距离即点![]() 到平面
到平面![]() 的距离,则可得到点
的距离,则可得到点![]() 到平面
到平面![]() 的距离为
的距离为![]() ;对于C,三棱锥
;对于C,三棱锥![]() 的外接球即四棱锥
的外接球即四棱锥![]() 的外接球,可得四棱锥
的外接球,可得四棱锥![]() 的高为
的高为![]() ,从而求得外接球的半径为
,从而求得外接球的半径为![]() .得外接球的表面积
.得外接球的表面积![]() ;对于D,连接
;对于D,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,
, ![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角,
所成的角,![]() .
.
解:如图,对于A,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 为
为![]() 与
与![]() 所成的角,
所成的角,
∵![]() ,
,![]() ,
, ![]() ,故A错误;
,故A错误;
对于B,由于![]() 平面
平面![]() ,故
,故![]() 到平面
到平面![]() 的距离即点
的距离即点![]() 到平面
到平面![]() 的距离,
的距离,
连接![]() 交
交![]() 于
于![]() ,可得
,可得![]() 平面
平面![]() ,而
,而![]() ,∴点
,∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,故B错误;
,故B错误;
对于C,三棱锥![]() 的外接球即四棱锥
的外接球即四棱锥![]() 的外接球,
的外接球,
∵![]() 为矩形,且
为矩形,且![]() ,
,![]() ,
, ![]() ,四棱锥
,四棱锥![]() 的高为
的高为![]() ,
,
设四棱锥![]() 的外接球的半径为
的外接球的半径为![]() ,则
,则![]() ,解得
,解得![]() .
.
∴三棱锥的外接球的表面积![]() ,故C错误;
,故C错误;
对于D,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角,在直角三角形
所成的角,在直角三角形![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() ,故D正确.
,故D正确.
故选:D


科目:高中数学 来源: 题型:
【题目】已知△![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,__________,求△
,__________,求△![]() 的周长
的周长![]() 和面积
和面积![]() .
.
在①![]() ,
,![]() ,②
,②![]() ,
,![]() ,③
,③![]() ,
,![]() 这三个条件中,任选一个补充在上面问题中的横线处,并加以解答.
这三个条件中,任选一个补充在上面问题中的横线处,并加以解答.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线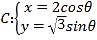 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程
的极坐标方程![]() ,点
,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为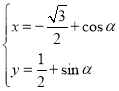 (
(![]() 为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(1)设射线l的极坐标方程为![]() ,若射线l与曲线C交于A,B两点,求AB的长;
,若射线l与曲线C交于A,B两点,求AB的长;
(2)设M,N是曲线C上的两点,若∠MON![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
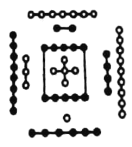
【题目】《易·系辞上》有“河出图,洛出书”之说.河图、洛书是中国古代流传下来的两幅神秘图案,蕴含了深奥的宇宙星象之理,被誉为“宇宙魔方”,是中华文化,阴阳术数之源.其中河图的排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中,如图,白圈为阳数,黑点为阴数,若从阴数和阳数中各取一数,则其差的绝对值为1的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com