
 将一张2×6米的硬钢板按图纸的要求进行操作,沿线裁去阴影部分,把剩余部分按要求焊接成一个有盖的长方体水箱(其中①与③、②与④分别是全等的矩形,且⑤+⑥=⑦),设水箱的高为x米,容积为y立方米.
将一张2×6米的硬钢板按图纸的要求进行操作,沿线裁去阴影部分,把剩余部分按要求焊接成一个有盖的长方体水箱(其中①与③、②与④分别是全等的矩形,且⑤+⑥=⑦),设水箱的高为x米,容积为y立方米.| 6-2x |
| 2 |
4±
| ||
| 3 |
4-
| ||
| 3 |
4-
| ||
| 3 |
4-
| ||
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
|
(1)写出y关于x的函数关系式;
(2)如何设计x的大小,使得水箱的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
将一张2×6米的硬钢板按图纸的要求进行操作:沿线裁去阴影部分,把剩余部分按要求焊接成一个有盖的长方体水箱(⑦为底,①②③④为侧面,⑤+⑥为水箱盖。其中①与③、②与④分别是全等的矩形,且⑤+⑥=⑦),设水箱的高为x米,容积为y立方米。

(1)写出y关于x的函数关系式;
(2)如何设计x的大小,使得水箱的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
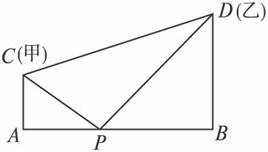
(1)设PA=x(x>0),试将x表示成送水需要的水管总长y的函数;
(2)问水站P建在什么位置,购买水管的费用最低?
(文)将一张2×6米的硬钢板按图纸的要求进行操作,沿线裁去阴影部分,把剩余部分按要求焊接成一个有盖的长方体水箱(其中①与③、②与④分别是全等的矩形,且⑤+⑥=⑦),设水箱的高为x米,容积为y立方米.
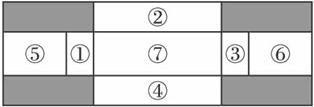
(1)求y关于x的函数关系式;
(2)如何设计x的大小,使得水箱装的水最多?
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)写出y关于x的函数关系式;
(2)如何设计x的大小,使得水箱的容积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com