
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.
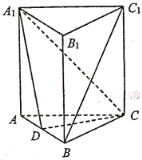
(1)求证:![]() ;
;
(2)求证:![]() .
.
【答案】(1)见详解;(2)见详解.
【解析】
(1)连接AC1,设AC1∩A1C=O,连接OD,可求O为AC1的中点,D是棱AB的中点,利用中位线的性质可证OD∥BC1,根据线面平行的判断定理即可证明BC1∥平面A1CD.
(2)由(1)可证平行四边形ACC1A1是菱形,由其性质可得AC1⊥A1C,利用线面垂直的性质可证AB⊥AA1,根据AB⊥AC,利用线面垂直的判定定理可证AB⊥平面ACC1A1,利用线面垂直的性质可证AB⊥A1C,又AC1⊥A1C,根据线面垂直的判定定理可证A1C⊥平面ABC1,利用线面垂直的性质即可证明BC1⊥A1C.
(1)连接AC1,设AC1∩A1C=O,连接OD,在直三棱柱ABC﹣A1B1C1中,侧面ACC1A1是平行四边形,
所以:O为AC1的中点,又因为:D是棱AB的中点,所以:OD∥BC1,
又因为:BC1平面A1CD,OD平面A1CD,所以:BC1∥平面A1CD.
(2)由(1)可知:侧面ACC1A1是平行四边形,因为:AC=AA1,所以:平行四边形ACC1A1是菱形,
所以:AC1⊥A1C,在直三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,因为:AB平面ABC,所以:AB⊥AA1,
又因为:AB⊥AC,AC∩AA1=A,AC平面ACC1A1,AA1平面ACC1A1,
所以:AB⊥平面ACC1A1,因为:A1C平面ACC1A1,所以:AB⊥A1C,
又因为:AC1⊥A1C,AB∩AC1=A,AB平面ABC1,AC1平面ABC1,所以:A1C⊥平面ABC1,
因为:BC1平面ABC1,所以:BC1⊥A1C.



科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投人某种产品的宣传费,需了解年宣传费![]() 对年销售额(单位:万元)的影响,对近6年的年宣传费
对年销售额(单位:万元)的影响,对近6年的年宣传费![]() 和年销售额
和年销售额![]() 数据进行了研究,发现宣传费
数据进行了研究,发现宣传费![]() 和年销售额
和年销售额![]() 具有线性相关关系,并对数据作了初步处理,得到下面的一些统计量的值.
具有线性相关关系,并对数据作了初步处理,得到下面的一些统计量的值.

(I)根据表中数据建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅱ)利用(I)中的回归方程预测该公司如果对该产品的宜传费支出为10万元时销售额是![]() 万元,该公司计划从10名中层管理人员中挑选3人担任总裁助理,10名中层管理人员中有2名是技术部骨干,记所挑选3人中技术部骨干人数为
万元,该公司计划从10名中层管理人员中挑选3人担任总裁助理,10名中层管理人员中有2名是技术部骨干,记所挑选3人中技术部骨干人数为![]() 且随机变量
且随机变量![]() ,求
,求![]() 的概率分布列与数学期望.
的概率分布列与数学期望.
附:回归直线的倾斜率截距的最小二乘估计公式分别为:
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=  ,设a∈R,若关于x的不等式f(x)≥|
,设a∈R,若关于x的不等式f(x)≥| ![]() +a|在R上恒成立,则a的取值范围是( )
+a|在R上恒成立,则a的取值范围是( )
A.[﹣ ![]() ,2]
,2]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣2 ![]() ,2]
,2]
D.[﹣2 ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
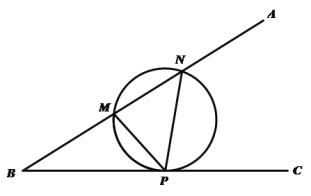
【题目】米勒问题,是指德国数学家米勒1471年向诺德尔教授提出的有趣问题:在地球表面的什么部位,一根垂直的悬杆呈现最长(即可见角最大?)米勒问题的数学模型如下:如图,设![]() 是锐角
是锐角![]() 的一边
的一边![]() 上的两定点,点
上的两定点,点![]() 是边
是边![]() 边上的一动点,则当且仅当
边上的一动点,则当且仅当![]() 的外接圆与边
的外接圆与边![]() 相切时,
相切时,![]() 最大.若
最大.若![]() ,点
,点![]() 在
在![]() 轴上,则当
轴上,则当![]() 最大时,点
最大时,点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=excosx﹣x.(13分)
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)在区间[0, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com