
【题目】在三棱锥A﹣BCD中,△ABD和△ACD是边长为2的等边三角形,![]() ,O、E分别是BC、AC的中点.
,O、E分别是BC、AC的中点.
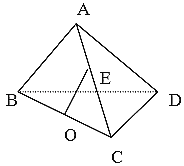
(1)求证:OE∥平面ABD;
(2)求证:平面ABC⊥平面BCD;
(3)求三棱锥A﹣BCD的表面积.
【答案】(1)见解析(2)见解析(3)4+2![]() .
.
【解析】
(1)由O、E分别是BC、AC的中点,可得OE∥AB,由线面平行的判定定理可得OE∥平面ABD;
(2)连接AO,DO,可得AO⊥BC,DO⊥BC,可得∠AOD为二面角A﹣BC﹣D的平面角,由已知条件可得∠AOD=90°,则平面ABC⊥平面BCD;
(3)分别计算出S△ABC、S△ABD、S△ACD、S△CBD,相加可得求三棱锥A﹣BCD的表面积.
(1)证明:O、E分别是BC、AC的中点,可得OE∥AB,
OE平面ABD,AB平面ABD,可得OE∥平面ABD;
(2)证明:连接AO,DO,
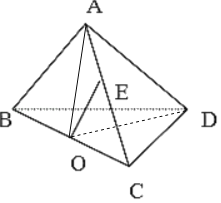
由AB=AC=BD=DC=2,可得AO⊥BC,DO⊥BC,
可得∠AOD为二面角A﹣BC﹣D的平面角,
由BC=2![]() ,可得AO=DO
,可得AO=DO![]() ,
,
在△AOD中,AO2+DO2=AD2,
可得∠AOD=90°,
则平面ABC⊥平面BCD;
(3)三棱锥A﹣BCD的表面积为S△ABC+S△ABD+S△ACD+S△CBD![]() 2×2
2×2![]() 22
22![]() 22
22![]() 2×2=4+2
2×2=4+2![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是两条异面直线,直线
是两条异面直线,直线![]() 与
与![]() 都垂直,则下列说法正确的是( )
都垂直,则下列说法正确的是( )
A. 若![]() 平面
平面![]() ,则
,则![]()
B. 若![]() 平面
平面![]() ,则
,则![]() ,
,![]()
C. 存在平面![]() ,使得
,使得![]() ,
,![]() ,
,![]()
D. 存在平面![]() ,使得
,使得![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱柱![]() 的主视图和俯视图如图所示(图中一格为单位正方形),D、D1分别为棱AC和A1C1的中点.
的主视图和俯视图如图所示(图中一格为单位正方形),D、D1分别为棱AC和A1C1的中点.
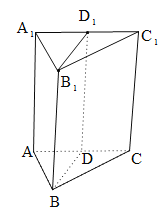
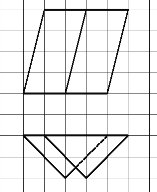
(1)求侧(左)视图的面积,并证明平面A1ACC1⊥平面B1BDD1
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,
,![]() ,②
,②![]() ,
,![]() ,③
,③![]() ,
,![]() 三个条件中任选一个补充在下面问题中,并加以解答.
三个条件中任选一个补充在下面问题中,并加以解答.
已知![]() 的内角A,B,C的对边分别为a,b,c,若
的内角A,B,C的对边分别为a,b,c,若![]() ,______,求
,______,求![]() 的面积S.
的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,焦距为2.
,焦距为2.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 的另一个交点为点
的另一个交点为点![]() ,与圆
,与圆![]() 的另一个交点为点
的另一个交点为点![]() ,是否存在直线
,是否存在直线![]() 使得
使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() ,
,![]() 是曲线
是曲线![]() 上的任意一点,动点
上的任意一点,动点![]() 满足
满足![]()
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)经过点![]() 的动直线
的动直线![]() 与点
与点![]() 的轨迹方程交于
的轨迹方程交于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() (异于点
(异于点![]() ),使得
),使得![]() ?若存在,求出
?若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面坐标系中xOy中,已知直线l的参数方程为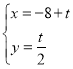 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为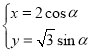 (
(![]() 为参数).以O为极点,x轴的非负半轴为极轴,建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴,建立极坐标系.
(1)求曲线C的普通方程和直线l的极坐标方程;
(2)设P为曲线C上的动点,求点P到直线l的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上任一点
上任一点![]() 到
到![]() ,
,![]() 的距离之和为4.
的距离之和为4.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,设直线
,设直线![]() 不经过
不经过![]() 点,
点,![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,若直线
两点,若直线![]() 的斜率与直线
的斜率与直线![]() 的斜率之和为
的斜率之和为![]() ,判断直线
,判断直线![]() 是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解居民的用电情况,某地供电局抽查了该市若干户居民月均用电量(单位:![]() ),并将样本数据分组为
),并将样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示.
,其频率分布直方图如图所示.
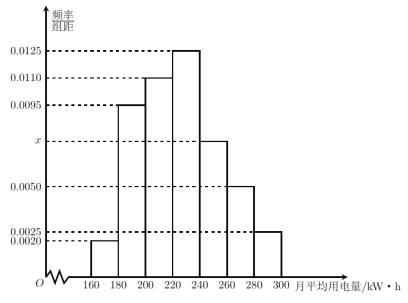
(1)若样本中月均用电量在![]() 的居民有
的居民有![]() 户,求样本容量;
户,求样本容量;
(2)求月均用电量的中位数;
(3)在月均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组居民中,用分层随机抽样法抽取
的四组居民中,用分层随机抽样法抽取![]() 户居民,则月均用电量在
户居民,则月均用电量在![]() 的居民应抽取多少户?
的居民应抽取多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com