
【题目】已知数列{an}的各项均为正数,前n和为Sn , 且Sn= ![]() (n∈N*).
(n∈N*).
(1)求证:数列{an}是等差数列;
(2)设bn=an3n , 求数列{bn}的前n项的和Tn .
【答案】
(1)
解:证明:当n≥2时, ![]() .…①
.…①
![]() …②
…②
①﹣②得: ![]() ,
,
整理得:(an+an﹣1)(an﹣an﹣1)=(an+an﹣1).
∵数列{an}的各项均为正数,即an+an﹣1≠0,
∴an﹣an﹣1=1(n≥2).
当n=1时, ![]() ,得
,得 ![]() ,
,
由a1>0,得a1=2,…(4分)
∴数列{an}是首项为2,公差为1的等差数列.
(2)
解:由(1)得an=2+(n﹣1)×1=n+1
∴ ![]()
![]() …(1)
…(1)
![]() …+n×3n+(n+1)×3n+1…(2)
…+n×3n+(n+1)×3n+1…(2)
(1)﹣(2)得 ![]()
∴ ![]()
∴ ![]()
【解析】(1)当当n≥2时,求得Sn及Sn﹣1 , 做差求得: ![]() 整理得:(an+an﹣1)(an﹣an﹣1)=(an+an﹣1)由an+an﹣1≠0,即可得到an﹣an﹣1=1,当n=1时,求得a1=2即可得数列{an}是等差数列;(2)由(1)求得数列{an}的通项公式,数列{bn}的前n项和Tn , 采用乘以公比“错位相减法”,即可求得Tn .
整理得:(an+an﹣1)(an﹣an﹣1)=(an+an﹣1)由an+an﹣1≠0,即可得到an﹣an﹣1=1,当n=1时,求得a1=2即可得数列{an}是等差数列;(2)由(1)求得数列{an}的通项公式,数列{bn}的前n项和Tn , 采用乘以公比“错位相减法”,即可求得Tn .
【考点精析】解答此题的关键在于理解等差数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() 或
或![]() ,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系
,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系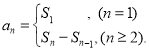 .
.


科目:高中数学 来源: 题型:
【题目】设F1(﹣c,0)、F2(c,0)是椭圆 ![]() =1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1 , 则椭圆的离心率为( )
=1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1 , 则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]在平面坐标系中xOy中,已知直线l的参考方程为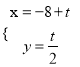 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为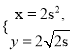 (s为参数)。设p为曲线C上的动点,求点P到直线l的距离的最小值
(s为参数)。设p为曲线C上的动点,求点P到直线l的距离的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一元二次不等式ax2+bx+c>0的解集是(﹣ ![]() ,2),则cx2+bx+a<0的解集是( )
,2),则cx2+bx+a<0的解集是( )
A.(﹣3, ![]() )
)
B.(﹣∞,﹣3)∪( ![]() ,+∞)
,+∞)
C.(﹣2, ![]() )
)
D.(﹣∞,﹣2)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱柱ABC﹣A1B1C1的侧面AA1C1C为正方形,侧面AA1B1B⊥侧面BB1C1C,且AC=2,AB= ![]() ,∠A1AB=45°,E、F分别为AA1、CC1的中点.
,∠A1AB=45°,E、F分别为AA1、CC1的中点. 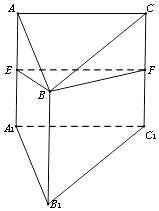
(1)求证:AA1⊥平面BEF;
(2)求二面角B﹣EB1﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,下顶点为
,下顶点为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)设![]() 为椭圆上异于其顶点的一点,
为椭圆上异于其顶点的一点, ![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且三角形
,且三角形![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相切,过焦点
相切,过焦点![]() ,
, ![]() 分别作
分别作![]() ,
, ![]() ,垂足分别为
,垂足分别为![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的外接圆半径为1,角A,B,C的对边分别为a,b,c,且2acosA=ccosB+bcosC.
(1)求cosA及a的值;
(2)若b2+c2=4,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com