
【题目】已知函数![]() (
(![]() 为自然对数的底数)
为自然对数的底数)
(Ⅰ)试讨论函数![]() 的零点个数;
的零点个数;
(Ⅱ)证明:当![]() 且
且![]() 时,总有
时,总有![]()
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)先求函数![]() 导数,根据导函数零点确定函数单调性:先增后减再增,结合图像可知零点个数按两极值正负分情况进行讨论,(2)先研究差函数
导数,根据导函数零点确定函数单调性:先增后减再增,结合图像可知零点个数按两极值正负分情况进行讨论,(2)先研究差函数![]() ,根据导数可得
,根据导数可得![]() ,导函数的导数
,导函数的导数![]() ,因此
,因此![]() ,从而
,从而![]() ,得证.
,得证.
试题解析:解:(Ⅰ) ![]() 零点个数即为方程
零点个数即为方程![]() 的根的个数.
的根的个数.
记![]() ,则
,则![]() ,令
,令![]() 得
得![]() 或
或![]() .
.
当![]() 变化时,
变化时, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
| 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
故可画出![]() 的草图如图所示:
的草图如图所示:

由图象知:当![]() 或
或![]() 时,函数
时,函数![]() 有一个零点;
有一个零点;
当![]() 或
或![]() 时,函数
时,函数![]() 有两个零点;
有两个零点;
当![]() 时,函数
时,函数![]() 有三个零点.
有三个零点.
(Ⅱ)![]() ,设函数
,设函数![]() ,
,
则![]() ,
,
记![]() ,则
,则![]() ,
,
当![]() 变化时,
变化时, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| 单调递减 | 极小值 | 单调递增 |
由上表可知![]() ,而
,而![]() ,
,
由![]() 知,
知, ![]() .
.
所以![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() 在区间
在区间![]() 上为增函数,
上为增函数,
所以当![]() 时,
时, ![]() .
.
即当![]() 且
且![]() 时,
时, ![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中,
中, ![]() 是椭圆的左、右焦点,过
是椭圆的左、右焦点,过![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,若
两点,若![]() 的周长为8,离心率为
的周长为8,离心率为![]() .
.
(1)求椭圆方程;
(2)若弦![]() 的斜率不为0,且它的中垂线与
的斜率不为0,且它的中垂线与![]() 轴交于
轴交于![]() ,求
,求![]() 的纵坐标的范围;
的纵坐标的范围;
(3)是否在![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣a(1﹣ ![]() ).
).
(1)若a=1,求f(x)的单调区间;
(2)若f(x)≥0,对任意的x≥1均成立,求实数a的取值范围;
(3)求证:( ![]() )1008>
)1008> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取![]() 名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试,测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子停下所需要的距离),无酒状态与酒后状态下的试验数据分别列于表
名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试,测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子停下所需要的距离),无酒状态与酒后状态下的试验数据分别列于表![]()
停车距离 |
|
|
|
|
|
频数 | 26 |
|
| 8 | 2 |
表![]()
平均每毫升血液酒精含量 | 10 | 30 | 50 | 70 | 90 | /tr>
平均停车距离 | 30 | 50 | 60 | 70 | 90 |
已知表![]() 数据的中位数估计值为
数据的中位数估计值为![]() ,回答以下问题.
,回答以下问题.
(Ⅰ)求![]() 的值,并估计驾驶员无酒状态下停车距离的平均数;
的值,并估计驾驶员无酒状态下停车距离的平均数;
(Ⅱ)根据最小二乘法,由表![]() 的数据计算
的数据计算![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(Ⅲ)该测试团队认为:驾驶员酒后驾车的平均“停车距离”![]() 大于(Ⅰ)中无酒状态下的停车距离平均数的
大于(Ⅰ)中无酒状态下的停车距离平均数的![]() 倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
(附:回归方程![]() 中,
中, 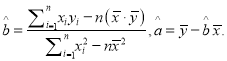 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行抽奖活动,规则如下:甲箱子里装有3个白球和2个黑球,乙箱子里装有1个白球和3个黑球,这些球除颜色外完全相同;每次抽奖都从这两个箱子里各随机地摸出2个球,若摸出的白球个数不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)在一次游戏中,求获奖的概率;
(2)在三次游戏中,记获奖次数为随机变量X,求X的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣a)2lnx(a为常数).
(1)若f(x)在(1,f(1))处的切线与直线2x+2y﹣3=0垂直.
(ⅰ)求实数a的值;
(ⅱ)若a非正,比较f(x)与x(x﹣1)的大小;
(2)如果0<a<1,判断f(x)在(a,1)上是否有极值,若有极值是极大值还是极小值?若无极值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知映射f:A→B,其中A=B=R,对应法则f:x→y=( ![]() )
) ![]() ,若对实数m∈B,在集合A中存在元素与之对应,则m的取值范围是( )
,若对实数m∈B,在集合A中存在元素与之对应,则m的取值范围是( )
A.(﹣∞,2]
B.[2,+∞)
C.(2,+∞)
D.(0,2]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com