
 <φ<
<φ< )的图象与x轴交点为(-
)的图象与x轴交点为(- ,0),与此交点距离最小的最高点坐标为(
,0),与此交点距离最小的最高点坐标为( ,1).
,1). 个单位,再把纵坐标伸长为原来的两倍,最后向上平移一个单位得到函数y=g(x)的图象.若对任意的0≤m≤3,方程|g(kx)|=m在区间[0,
个单位,再把纵坐标伸长为原来的两倍,最后向上平移一个单位得到函数y=g(x)的图象.若对任意的0≤m≤3,方程|g(kx)|=m在区间[0, ]上至多有一个解,求正数k的取值范围.
]上至多有一个解,求正数k的取值范围. +
+ )=π,可求ω,由f(-
)=π,可求ω,由f(- )=0及-
)=0及-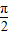 <φ<
<φ< 可得φ;
可得φ; +
+ )=π,而T=
)=π,而T= ,则ω=2,
,则ω=2, 时,y=0,所以sin(2×(-
时,y=0,所以sin(2×(- )+φ)=0,而-
)+φ)=0,而- <φ<
<φ< ,则φ=
,则φ= ,
,
 );
); )的周期为π,
)的周期为π, )在[0,2π]内恰有2个周期,并且方程sin(2x+
)在[0,2π]内恰有2个周期,并且方程sin(2x+ )=a(-1<a<0)在[0,2π]内有4个实根,
)=a(-1<a<0)在[0,2π]内有4个实根, ,
, ,
, ;
; )+1,
)+1, .
.

科目:高中数学 来源: 题型:
| a-x2 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com