
【题目】某手机生产企业为了解消费者对某款手机的认同情况,通过销售部随机抽取50名购买该款手机的消费者,并发出问卷调查(满分50分),该问卷只有20份给予回复,这20份的评分如下:
男 | 47,36,28,48,48,44,50,46,50,37,35,49 |
女 | 38,37,50,36,38,45,29,39 |
(1)完成下面的茎叶图,并求12名男消费者评分的中位数与8名女消费者评分的众数及平均值;
男 | 女 | |
2 | ||
3 | ||
4 | ||
5 |
满意 | 不满意 | 合计 | |
男 | |||
女 | |||
合计 |
(2)若大于40分为“满意”,否则为“不满意”,完成上面的![]() 列联表,并判断是否有95%的把握认为消费者对该款手机的“满意度”与性别有关;
列联表,并判断是否有95%的把握认为消费者对该款手机的“满意度”与性别有关;
(3)若从回复的20名消费者中按性别用分层抽样的方法抽取5人,再从这5人中随机抽取2人作进一步调查,求至少有1名女性消费者被抽到的概率.
附:
| 0.05 | 0.025 | 0.01 |
| 3.841 | 5.024 | 6.635 |
【答案】(1)见解析,男消费者评分的中位数是46.5,众数为38,平均值39;(2)见解析,没有;(3)![]()
【解析】
(1)根据题意填写茎叶图,根据中位数,众数和平均数计算方法求解即可;
(2)根据题意填写![]() 列联表,计算
列联表,计算![]() 的值,对照临界值,作出判断即可;
的值,对照临界值,作出判断即可;
(3)根据古典概型计算公式计算即可.
(1)茎叶图如图
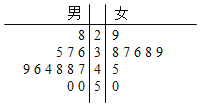
由图可知,12名男消费者评分的中位数是![]() 46.5;
46.5;
女消费者评分的众数为![]() ,平均值为
,平均值为![]() ,
,
(2)列联表如图,
满意 | 不满意 | 合计 | |
男 | 8 | 4 | 12 |
女 | 2 | 6 | 8 |
合计 | 10 | 10 | 20 |
![]() ,
,
所以没有95%的把握认为消费者对该款手机的“满意度”与性别有关.
(3)由题意可得抽取的5人中3名男生设为a,b,c,2名女生设为A,B,
抽取总数有(a,b),(a,c),(a,A),(a,B),(b,c),(b,A),(b,B),(c,A),(c,B),(A,B)10种,
其中至少有1名女性消费者的7种,
故所求的概率为P![]() .
.


科目:高中数学 来源: 题型:
【题目】某个比赛安排4名志愿者完成6项工作,每人至少完成一项,每项工作由一人完成,则不同的安排方式有多少种( )
A.7200种B.4800种C.2640种D.1560种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生活中万事万物都是有关联的,所有直线中有关联直线,所有点中也有相关点,现在定义:平面内如果两点![]() 、
、![]() 都在函数
都在函数![]() 的图像上,而且满足
的图像上,而且满足![]() 、
、![]() 两点关于原点对称,则称点对(
两点关于原点对称,则称点对(![]() 、
、![]() )是函数
)是函数![]() 的“相关对称点对”(注明:点对(
的“相关对称点对”(注明:点对(![]() 、
、![]() )与(
)与(![]() 、
、![]() )看成同一个“相关对称点对”).已知函数
)看成同一个“相关对称点对”).已知函数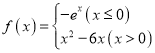 ,则这个函数的“相关对称点对”有( )
,则这个函数的“相关对称点对”有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,摩天轮的半径为![]() ,
,![]() 点距地面的高度为
点距地面的高度为![]() ,摩天轮按逆时针方向作匀速运动,且每
,摩天轮按逆时针方向作匀速运动,且每![]() 转一圈,摩天轮上点
转一圈,摩天轮上点![]() 的起始位置在最高点.
的起始位置在最高点.

(1)试确定点![]() 距离地面的高度
距离地面的高度![]() (单位:
(单位:![]() )关于旋转时间
)关于旋转时间![]() (单位:
(单位:![]() )的函数关系式;
)的函数关系式;
(2)在摩天轮转动一圈内,有多长时间![]() 点距离地面超过
点距离地面超过![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 与点
与点![]() 在直线
在直线![]() 的两侧,给出以下结论:①
的两侧,给出以下结论:① ![]() ;② 当
;② 当![]() 时,
时,![]() 有最小值,无最大值;③
有最小值,无最大值;③ ![]() ;④ 当
;④ 当![]() 且
且![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;正确的个数是( )
;正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com