
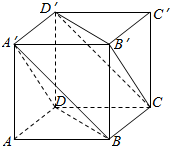
 正方体ABCD-A′B′C′D′棱长为1
正方体ABCD-A′B′C′D′棱长为1分析 (1)先证明四边形BB′D′D是平行四边形,可得D′B′∥面A′BD,同理证明B′C∥面A′BD,从而利用两个平面平行的判定定理证得面A′BD∥面B′CD′.
(2)利用等体积法,求点B′到面A′BD的距离.
解答 (1)证明:∵B′B平行且等于A′A,A′A平行且等于D′D,
∴B′B平行且等于D′D,
∴四边形BB′D′D是平行四边形,
∴D′B′∥DB,
∵D′B′?面A′BD,DB?面A′BD,
∴D′B′∥面A′BD,
同理B′C∥面A′BD,
∵D′B′∩B′C=B′,
∴面A′BD∥面B′CD′.
(2)解:设点B′到面A′BD的距离为h,则
∵△A′BD的面积S=$\frac{\sqrt{3}}{4}$,
∴由等体积可得$\frac{1}{3}×\frac{\sqrt{3}}{4}$h=$\frac{1}{3}×\frac{1}{2}×1×1×1$,∴h=$\frac{2\sqrt{3}}{3}$.
点评 本题主要考查直线和平面平行、平面和平面平行的判定定理的应用,考查点到平面的距离,属于中档题.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-1 | B. | $\sqrt{3}$-1 | C. | 2$\sqrt{2}$-2 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
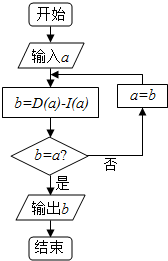 已知集合A-{1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )
已知集合A-{1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )| A. | 792 | B. | 693 | C. | 594 | D. | 495 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com