
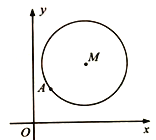
【题目】如图,在平面直角坐标系![]() 中,已知以
中,已知以![]() 为圆心的圆
为圆心的圆![]() 及其上一点
及其上一点![]() .
.
(1)设圆![]() 与
与![]() 轴相切,与圆
轴相切,与圆![]() 外切,且圆心
外切,且圆心![]() 在直线
在直线![]() 上,求圆
上,求圆![]() 的标准方程;
的标准方程;
(2)设平行于![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】某医药研究所开发一种新药,如果成年人按规定的剂量服用,据监测,服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.据进一步测定,每毫升血液中含药量不少于0.25微克时,治疗疾病有效,则服药一次治疗该疾病有效的时间为( ) 
A.4小时
B.![]()
C.![]()
D.5小时
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(﹣1,1)上的函数f(x)满足:对任意x,y∈(﹣1,1)都有f(x)+f(y)=f(x+y).
(Ⅰ)求证:函数f(x)是奇函数;
(Ⅱ)如果当x∈(﹣1,0]时,有f(x)<0,试判断f(x)在(﹣1,1)上的单调性,并用定义证明你的判断;
(Ⅲ)在(Ⅱ)的条件下,若a﹣8x+1>0对满足不等式f(x﹣ ![]() )+f(
)+f( ![]() ﹣2x)<0的任意x恒成立,求a的取值范围.
﹣2x)<0的任意x恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种产品,第一年投入资金1000万元,出售产品收入40万元,预计以后每年的投入资金是上一年的一半,出售产品所得收入比上一年多80万元,同时,当预计投入的资金低于20万元时,就按20万元投入,且当年出售产品收入与上一年相等.
(1)求第![]() 年的预计投入资金与出售产品的收入;
年的预计投入资金与出售产品的收入;
(2)预计从哪一年起该公司开始盈利?(注:盈利是指总收入大于总投入)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为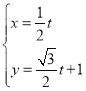 (
(![]() 为参数),曲线
为参数),曲线![]() 的普通方程为
的普通方程为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(I)求直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的参数方程;
的参数方程;
(II)设点D在曲线![]() 上,且曲线
上,且曲线![]() 在点D处的切线与直线
在点D处的切线与直线![]() 垂直,试确定点D的坐标.
垂直,试确定点D的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判定f(x)的奇偶性并证明;
(Ⅲ)用函数单调性定义证明:f(x)在(1,+∞)上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意实数x,不等式ax2+2ax﹣(a+2)<0恒成立,则实数a的取值范围是( )
A.﹣1≤a≤0
B.﹣1≤a<0
C.﹣1<a≤0
D.﹣1<a<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com