Question

12．已知动圆Q过定点F（0，-1），且与直线y=1相切；椭圆N的对称轴为坐标轴，中心为坐标原点O，F是其一个焦点，又点（0，2）在椭圆N上．
（1）求动圆圆心Q的轨迹M的方程和椭圆N的方程；
（2）过点（0，-4）作直线l交轨迹M于A，B两点，连结OA，OB，射线OA，OB交椭圆N于C，D两点，求△OCD面积的最小值．
（3）附加题（本题额外加5分）：过椭圆N上一动点P作圆x²+（y-1）²=1的两条切线，切点分别为G，H，求$\overrightarrow{PG}•\overrightarrow{PH}$的取值范围．

Answer 1

分析 （1）由抛物线的定义可得动点Q的轨迹M的标准方程，由题意可得c=1，a=2，求得b，进而得到椭圆方程；
（2）显然直线m的斜率存在，不妨设直线m的直线方程为：y=kx-4，分别代入抛物线方程和椭圆方程，运用韦达定理和弦长公式，以及点到直线的距离公式，求得三角形的面积，再由不等式的性质，即可得到所求最小值．
（3）设∠EPF=2α，求出$\overrightarrow{PG}•\overrightarrow{PH}$表达式，利用$\left|\overrightarrow{PG}\right|$的范围，求解表达式的范围即可．

解答 解：（1）依题意，由抛物线的定义易得动点Q的轨迹M的标准方程为：x²=-4y，
依题意可设椭圆N的标准方程为$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0），
显然有c=1，a=2∴b=$\sqrt{3}$，
∴椭圆N的标准方程为：$\frac{{y}^{2}}{4}+\frac{{x}^{2}}{3}=1$；
轨迹$M：{x^2}=-4y，N：\frac{y^2}{4}+\frac{x^2}{3}=1$；
（2）$\left\{\begin{array}{l}y=kx-4\\{x^2}=-4y\end{array}\right.⇒{x^2}-4kx-16=0⇒\left\{\begin{array}{l}{x_1}+{x_2}=4k\\{x_1}{x_2}=-16\\{y_1}{y_2}=16\end{array}\right.$
所以x₁x₂+y₁y₂=0⇒OA⊥OB
设$OM：\left\{\begin{array}{l}y=kx\\ 3{y^2}+4{x^2}=12\end{array}\right.⇒（3{k^2}+4）{x^2}=12⇒{x_M}^2=\frac{12}{{3{k^2}+4}}$，
所以$|{OM}|=\sqrt{1+{k^2}}|{x_M}|=\sqrt{1+{k^2}}\sqrt{\frac{12}{{3{k^2}+4}}}$，
同理可得：$|{ON}|=\sqrt{1+\frac{1}{k^2}}|{x_N}|=\sqrt{\frac{{1+{k^2}}}{k^2}}\sqrt{\frac{{12{k^2}}}{{3+4{k^2}}}}$，
所以${S_{△OMN}}=\frac{1}{2}|{OM}|•|{ON}|=6\sqrt{\frac{{{{（1+{k^2}）}^2}}}{{（3{k^2}+4）（3+4{k^2}）}}}$，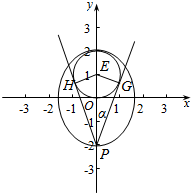
令t=1+k²（t≥1），${S_△}=6\sqrt{\frac{t^2}{{12{t^2}+t-1}}}=6\sqrt{\frac{1}{{-{{（\frac{1}{t}-\frac{1}{2}）}^2}+\frac{49}{4}}}}$，
所以当$t=2，即：k=±1时，{S_{max}}=\frac{12}{7}$
（3）（附加题）设∠GPH=2α，圆x²+（y-1）²=1的圆心为E，如图：
当P在椭圆上顶点时PE最小为1，在椭圆下顶点时，|PE|的最大值为3，PE∈[1，3]，
PEcosα=PG，sinα=$\frac{1}{PE}$．
∴${\;}\overrightarrow{PG}•\overrightarrow{PH}=|PG{|}^{2}cos2α=|PE{|}^{2}co{s}^{2}α•（1-2si{n}^{2}α）=|PE{|}^{2}（1-\frac{1}{{|PE|}^{2}}）（1-2\frac{1}{{|PE|}^{2}}）$
=$|PE{|}^{2}+\frac{2}{{|PE|}^{2}}-3$$≥2\sqrt{|PE{|}^{2}•\frac{2}{{|PE|}^{2}}}-3$=$2\sqrt{2}-4$，当且仅当|PE|=$\sqrt{2}$时取等号．
因为|PE|∈[1，3]，所以$\overrightarrow{PG}•\overrightarrow{PH}∈[2\sqrt{2}-3，\frac{56}{9}]$．

点评 本题考查直线和圆相切的条件，同时考查抛物线的定义和椭圆方程的运用，注意联立直线方程，运用韦达定理和弦长公式，考查化简整理的运算能力，属于难题．