
【题目】如图所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,FD⊥底面ABCD,M是AB的中点. 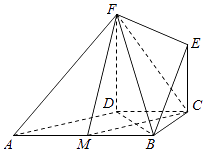
(1)求证:平面CFM⊥平面BDF;
(2)点N在CE上,EC=2,FD=3,当CN为何值时,MN∥平面BEF.
【答案】
(1)证明:∵FD⊥底面ABCD,∴FD⊥AD,FD⊥BD
∵AF=BF,∴△ADF≌△BDF,∴AD=BD,
连接DM,则DM⊥AB,
∵AB∥CD,∠BCD=90°,
∴四边形BCDM是正方形,∴BD⊥CM,
∵DF⊥CM,∴CM⊥平面BDF.
(2)解:当CN=1,即N是CE的中点时,MN∥平面BEF.
证明如下:
过N作NO∥EF,交ED于O,连结MO,

∵EC∥FD,∴四边形EFON是平行四边形,
∵EC=2,FD=3,∴OF=1,∴OD=2,
连结OE,则OE∥DC∥MB,且OE=DC=MB,
∴四边形BMOE是平行四边形,则OM∥BE,又OM∩ON=O,
∴平面OMN∥平面BEF,
∵MN平面OMN,∴MN∥平面BEF.
【解析】(1)推导出四边形BCDM是正方形,从而BD⊥CM,又DF⊥CM,由此能证明CM⊥平面BDF.(2)过N作NO∥EF,交EF于O,连结MO,则四边形EFON是平行四边形,连结OE,则四边形BMON是平行四边形,由此能推导出N是CE的中点时,MN∥平面BEF.
【考点精析】掌握直线与平面平行的判定和平面与平面垂直的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,D,E分别是BC,AC的中点.PB=PC=AB=2,AC=4,BC=2 ![]() ,PA=
,PA= ![]() .
. 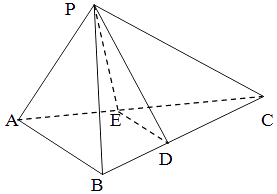
(1)求证:平面ABC⊥平面PED;
(2)求AC与平面PBC所成的角;
(3)求平面PED与平面PAB所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂修建一个长方体形无盖蓄水池,其容积为4800立方米,深度为3米.池底每平方米的造价为150元,池壁每平方米的造价为120元.设池底长方形长为x米.
(Ⅰ)求底面积并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:x2=2py(p>0),直线y=kx+2与E交于A、B两点,且 ![]() =2,其中O为原点.
=2,其中O为原点.
(1)求抛物线E的方程;
(2)点C坐标为(0,﹣2),记直线CA、CB的斜率分别为k1 , k2 , 证明:k12+k22﹣2k2为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A=[a﹣3,a],函数 ![]() (﹣2≤x≤5)的单调减区间为集合B.
(﹣2≤x≤5)的单调减区间为集合B.
(1)若a=0,求(RA)∪(RB);
(2)若A∩B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() +
+ ![]() )x3(a>0,a≠1).
)x3(a>0,a≠1).
(1)讨论函数f(x)的奇偶性;
(2)求a的取值范围,使f(x)+f(2x)>0在其定义域上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位要在800名员工中抽去80名员工调查职工身体健康状况,其中青年员工400名,中年员工300名,老年员工100名,下列说法错误的是( )
A.老年人应作为重点调查对象,故抽取的老年人应超过40名
B.每个人被抽到的概率相同为 ![]()
C.应使用分层抽样抽取样本调查
D.抽出的样本能在一定程度上反映总体的健康状况
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AA1=BC=2AC=2. (Ⅰ)若D为AA1中点,求证:平面B1CD⊥平面B1C1D;
(Ⅱ)在AA1上是否存在一点D,使得二面角B1﹣CD﹣C1的大小为60°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com