
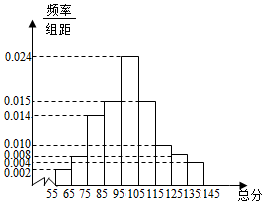
 从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.
从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.分析 (1)利用同一组中的数据用该组区间的中点值作代表,求这100份数学试卷的样本平均分$\overline x$和样本方差s2;
(2)利用互斥事件的概率公式,即可求解.
解答 解:(1)由题意,$\overline{x}$=60×0.02+70×0.08+80×0.14+90×0.15+100×0.24+110×0.15+120×0.1+130×0.08+140×0.04=100,
s2=(60-100)2×0.02+(70-100)2×0.08+(80-100)2×0.14+(90-100)2×0.15+(100-100)2×0.24+(110-100)2×0.15+(120-100)2×0.1+(130-100)2×0.08+(140-100)2×0.04=366;
(2)总分在[55,65)和[135,145)的试卷,共有6份试卷,其中[55,65)有2份,[135,145)有4份,
一份少于65分的概率为$\frac{8}{15}$,2份少于65分的概率为$\frac{1}{15}$,故抽取的2分试卷中至少有一份总分少于65分的概率为$\frac{8}{15}+\frac{1}{15}$=$\frac{3}{5}$.
点评 本题考查概率的计算,考查学生的计算能力,属于中档题.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:解答题
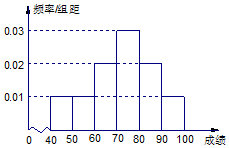 某校举办安全法规知识竞赛,从参赛的高一学生中抽出100人的成绩作为样本进行统计,并按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分组,得到成绩分布的频率分布直方图(如图).
某校举办安全法规知识竞赛,从参赛的高一学生中抽出100人的成绩作为样本进行统计,并按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分组,得到成绩分布的频率分布直方图(如图).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充要条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1} | B. | {-2,-1} | C. | {-2,-1} | D. | {-3,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 266,14 | B. | 256,14 | C. | 256,-$\frac{21}{4}$ | D. | 266,-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com