练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某综艺节目为比较甲、乙两名选手的各项能力(指标值满分为5分，分值高者为优)，绘制了如图所示的六维能力雷达图，图中点A表示甲的创造力指标值为4，点B表示乙的空间能力指标值为3，则下面叙述正确的是

    A. 乙的记忆能力优于甲的记忆能力

    B. 乙的创造力优于观察能力

    C. 甲的六大能力整体水平优于乙

    D. 甲的六大能力中记忆能力最差

    【答案】C

    【解析】

    从六维能力雷达图中我们可以得到甲的各种能力的大小、乙的各种能力的大小以及甲、乙的各项能力的大小关系等，从而可判断A，B，D.而整体水平的优劣取决于六种能力的数字之和的大小，计算可得孰优孰劣.

    从六维能力雷达图上可以得到甲的记忆能力优于乙的记忆能力，故A错.

    乙的创造力为3，观察能力为4，乙的观察能力优于创造力，故B错.

    甲的六大能力总和为，乙的六大能力总和为，

    故甲的六大能力整体水平优于乙，故C正确.

    甲的六大能力中，推理能力为3，为最差能力，故D错.

    综上，选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆C：x2＋y2＋2x－4y＋3＝0.

    （1）若圆C的切线在x轴和y轴上的截距相等，求此切线的方程．

    （2）点P在直线l：2x－4y＋3＝0上，过点P作圆C的切线，切点记为M，求使|PM|最小的点P的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2017年某市有2万多文科考生参加高考，除去成绩为分（含分）以上的3人与成绩为分（不含分）以下的3836人，还有约1.9万文科考生的成绩集中在内，其成绩的频率分布如下表所示：

    分数段

    频率

    0.108

    0.133

    0.161

    0.183

    分数段

    频率

    0.193

    0.154

    0.061

    0.007

    （Ⅰ）试估计该次高考成绩在内文科考生的平均分（精确到）；

    （Ⅱ）一考生填报志愿后，得知另外有4名同分数考生也填报了该志愿.若该志愿计划录取3人，并在同分数考生中随机录取，求该考生不被该志愿录取的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某自然资源探险组织试图穿越某峡谷，但峡谷内被某致命昆虫所侵扰，为了穿越这个峡谷，该探险组织进行了详细的调研，若每平方米的昆虫数量记为昆虫密度，调研发现，在这个峡谷中，昆虫密度是时间（单位：小时）的一个连续不间断的函数其函数表达式为

    ，

    其中时间是午夜零点后的小时数，为常数.

    （1）求的值；

    （2）求出昆虫密度的最小值和出现最小值的时间；

    （3）若昆虫密度不超过1250只/平方米，则昆虫的侵扰是非致命性的，那么在一天24小时内哪些时间段，峡谷内昆虫出现非致命性的侵扰.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆（）的右焦点为，右顶点为，已知，其中为原点，为椭圆的离心率.

    （Ⅰ）求椭圆的方程；

    （Ⅱ）设过点的直线与椭圆交于点（不在轴上），垂直于的直线与交于点，与轴交于点，若，且，求直线的斜率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了治理大气污染，某市2017年初采用了一系列措施，比如“煤改电”，“煤改气”，“整治散落污染企业”等．下表是该市2016年11月份和2017年11月份的空气质量指数（）（指数越小，空气质量越好）统计表．根据表中数据回答下列问题：

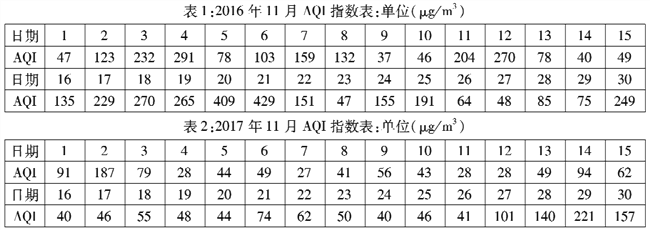
    （1）将2017年11月的空气质量指数数据用该天的对应日期作为样本编号，再用系统抽样方法从中抽取6个数据，若在2017年11月16日到11月20日这五天中用简单随机抽样抽取到的样本的编号是19号，写出抽出的样本数据；

    （2）从（1）中抽出的6个样本数据中随机抽取2个，求这2个数据之差的绝对值小于30的概率；

    （3）根据《环境空气质量指数（）技术规定（试行）》规定：当空气质量指数为（含50）时，空气质量级别为一级，求出这两年11月空气质量指数为一级的概率，你认为该市2017年初开始采取的这些大气污染治理措施是否有效？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）求出函数的定义域；

    （2）若当时，在上恒正，求出的取值范围；

    （3）若函数在上单调递增，求出的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中为常数.

    （1）当时，讨论的单调性；

    （2）当时，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题的便可提交通过.已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是,且每题正确完成与否互不影响.

    (1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算均值;

    (2)试从两位考生正确完成题数的均值及至少正确完成2题的概率分析比较两位考生的实验操作能力.

    查看答案和解析>>

    同步练习册答案