练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    圆(x＋2)2＋y2＝4与圆(x－2)2＋(y－1)2＝9的位置关系为(　　)．

    A．内切 B．相交 C．外切 D．相离

     

    ?B

    【解析】两圆的圆心分别为(－2,0)，(2,1)，半径分别为r＝2，R＝3两圆的圆心距离为＝，则R－r<<R＋r，所以两圆相交．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练选修4-1练习卷（解析版） 题型：填空题

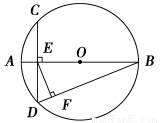
    如图所示，在圆O中，直径AB与弦CD垂直，垂足为E，EF⊥DB，垂足为F，若AB＝6，AE＝1，则DF·DB＝________.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-6-3练习卷（解析版） 题型：填空题

    已知椭圆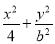＝1(0<b<2)与y轴交于A，B两点，点F为该椭圆的一个焦点，则△ABF面积的最大值为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-6-2练习卷（解析版） 题型：选择题

    抛物线y2＝4x的焦点到双曲线x2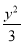－＝1的渐近线的距离是(　　)．

    A.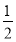 B.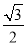 C．1 D.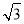

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-6-1练习卷（解析版） 题型：填空题

    直线y＝2x＋3被圆x2＋y2－6x－8y＝0所截得的弦长等于________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-5-3练习卷（解析版） 题型：填空题

    在四面体P－ABC中，PA，PB，PC两两垂直，设PA＝PB＝PC＝a，则点P到平面ABC的距离为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-5-2练习卷（解析版） 题型：解答题

    如图，在三棱柱ABC－A1B1C1中，CA＝CB，AB＝AA1，∠BAA1＝60°.

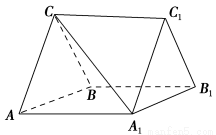
    (1)证明：AB⊥A1C；

    (2)若AB＝CB＝2，A1C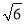＝，求三棱柱ABC－A1B1C1的体积；

    (3)若平面ABC⊥平面AA1B1B，AB＝CB＝2，求直线A1C与平面BB1C1C所成角的正弦值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-5-1练习卷（解析版） 题型：选择题

    某几何体的三视图如图所示，则该几何体的体积为(　　)．

    A．16＋8π B．8＋8π C．16＋16π D．8＋16π

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-3-1练习卷（解析版） 题型：填空题

    函数y＝tan ωx(ω＞0)与直线y＝a相交于A，B两点，且|AB|最小值为π，则函数f(x)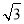＝sin ωx－cos ωx的单调增区间是________．

     

    查看答案和解析>>

    同步练习册答案