
ЁОЬтФПЁПФГЛЏЙЄГЇЩњВњМзЁЂввСНжжЛьКЯЗЪСЯЃЌашвЊAЃЌBЃЌCШ§жжжївЊдСЯЃЌЩњВњ1ГЖЦЄМзжжЗЪСЯКЭЩњВњ1ГЕЦЄввжжЗЪСЯЫљашШ§жждСЯЕФЖжЪ§ШчБэЫљЪОЃК
| A | B | C |
Мз | 4 | 8 | 3 |
вв | 5 | 5 | 10 |
ЯжгаAжждСЯ200ЖжЃЌBжждСЯ360ЖжЃЌCжждСЯ300ЖжЃЌдкДЫЛљДЁЩЯЩњВњМзЁЂввСНжжЗЪСЯЃЎвбжЊЩњВњ1ГЕЦЄМзжжЗЪСЯЃЌВњЩњЕФРћШѓЮЊ2ЭђдЊЃЛЩњВњ1ГЕЦЗввжжЗЪСЯЃЌВњЩњЕФРћШѓЮЊ3ЭђдЊЁЂЗжБ№гУxЃЌyБэЪОМЦЛЎЩњВњМзЁЂввСНжжЗЪСЯЕФГЕЦЄЪ§ЃЎ
ЃЈ1ЃЉгУxЃЌyСаГіТњзуЩњВњЬѕМўЕФЪ§бЇЙиЯЕЪНЃЌВЂЛГіЯргІЕФЦНУцЧјгђЃЛ
ЃЈ2ЃЉЮЪЗжБ№ЩњВњМзЁЂввСНжжЗЪСЯЃЌЧѓГіДЫзюДѓРћШѓЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКxЃЌyТњзуЕФЬѕМўЙиЯЕЪНЮЊЃК  ЃЎ
ЃЎ
зїГіЦНУцЧјгђШчЭМЫљЪОЃК
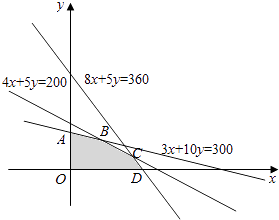
ЃЈ2ЃЉНтЃКЩшРћШѓЮЊzЭђдЊЃЌдђz=2x+3yЃЎ
Ёрy=Љ ![]() ЃЎ
ЃЎ
ЁрЕБжБЯпy=Љ ![]() ОЙ§ЕуBЪБЃЌНиОр
ОЙ§ЕуBЪБЃЌНиОр ![]() зюДѓЃЌМДzзюДѓЃЎ
зюДѓЃЌМДzзюДѓЃЎ
НтЗНГЬзщ ![]() ЕУBЃЈ20ЃЌ24ЃЉЃЎ
ЕУBЃЈ20ЃЌ24ЃЉЃЎ
ЁрzЕФзюДѓжЕЮЊ2ЁС20+3ЁС24=112ЃЎ
Д№ЃКЕБЩњВњМзжжЗЪСЯ20ЖжЃЌввжжЗЪСЯ24ЖжЪБЃЌРћШѓзюДѓЃЌзюДѓРћШѓЮЊ112ЭђдЊ
ЁОНтЮіЁПЃЈ1ЃЉИљОндСЯЕФЖжЪ§СаГіВЛЕШЪНзщЃЌзїГіЦНУцЧјгђЃЛЃЈ2ЃЉСюРћШѓz=2x+3yЃЌдђy=Љ ![]() ЃЌНсКЯПЩаагђевГізюгХНтЕФЮЛжУЃЌСаЗНГЬзщНтГізюгХНтЃЎ
ЃЌНсКЯПЩаагђевГізюгХНтЕФЮЛжУЃЌСаЗНГЬзщНтГізюгХНтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() .
.
ЃЈ1ЃЉЩшКЏЪ§![]() ЃЌШє
ЃЌШє![]() дкЧјМф
дкЧјМф![]() ЩЯЕЅЕїЃЌЧѓЪЕЪ§
ЩЯЕЅЕїЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЧѓжЄЃК ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕиЧјФтНЈСЂвЛИівеЪѕВЉЮяЙнЃЌВЩШЁОКБъЕФЗНЪНДгЖрМвНЈжўЙЋЫОбЁШЁвЛМвНЈжўЙЋЫОЃЌОЙ§ВуВуЩИбЁЃЌМзЁЂввСНМвНЈжўЙЋЫОНјШызюКѓЕФеаБъ.ЯжДгНЈжўЩшМЦдКЦИЧызЈМвЩшМЦСЫвЛИіеаБъЗНАИ:СНМвЙЋЫОДг![]() ИіеаБъЮЪЬтжаЫцЛњГщШЁ
ИіеаБъЮЪЬтжаЫцЛњГщШЁ![]() ИіЮЪЬтЃЌвбжЊет
ИіЮЪЬтЃЌвбжЊет![]() ИіеаБъЮЪЬтжаЃЌМзЙЋЫОПЩе§ШЗЛиД№ЦфжаЕФ
ИіеаБъЮЪЬтжаЃЌМзЙЋЫОПЩе§ШЗЛиД№ЦфжаЕФ![]() ЕРю}ФПЃЌЖјввЙЋЫОФме§ШЗЛиД№АЕРЬтФПЕФИХТЪОљЮЊ
ЕРю}ФПЃЌЖјввЙЋЫОФме§ШЗЛиД№АЕРЬтФПЕФИХТЪОљЮЊ![]() ЃЌМзЁЂввСНМвЙЋЫОЖдУПЬтЕФЛиД№ЖМЪЧЯрЛЅЖРСЂЃЌЛЅВЛгАЯьЕФ.
ЃЌМзЁЂввСНМвЙЋЫОЖдУПЬтЕФЛиД№ЖМЪЧЯрЛЅЖРСЂЃЌЛЅВЛгАЯьЕФ.
ЃЈ1ЃЉЧѓМзЁЂввСНМвЙЋЫОЙВД№Жд![]() ЕРЬтФПЕФИХТЪЃЛ
ЕРЬтФПЕФИХТЪЃЛ
ЃЈ2ЃЉЧыДгЦкЭћКЭЗНВюЕФНЧЖШЗжЮіЃЌМзЁЂввСНМвФФМвЙЋЫООКБъГЩЙІЕФПЩФмадИќДѓЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=cos2ІиxЉsin2Іиx+2 ![]() cosІиxsinІиxЃЌЦфжаІиЃО0ЃЌШєfЃЈxЃЉЯрСкСНЬѕЖдГЦжсМфЕФОрРыВЛаЁгк
cosІиxsinІиxЃЌЦфжаІиЃО0ЃЌШєfЃЈxЃЉЯрСкСНЬѕЖдГЦжсМфЕФОрРыВЛаЁгк ![]()
ЃЈ1ЃЉЧѓІиЕФШЁжЕЗЖЮЇМАКЏЪ§fЃЈxЃЉЕФЕЅЕїЕндіЧјМфЃЛ
ЃЈ2ЃЉдкЁїABCжаЃЌaЃЌbЃЌcЗжБ№ЪЧНЧAЃЌBЃЌCЕФЖдБпЃЌa= ![]() ЃЌb+c=3ЃЌЕБІизюДѓЪБЃЌfЃЈAЃЉ=1ЃЌЧѓsinBsinCЕФжЕЃЎ
ЃЌb+c=3ЃЌЕБІизюДѓЪБЃЌfЃЈAЃЉ=1ЃЌЧѓsinBsinCЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПе§ЫФРтзЖPЉABCDЃЌB1ЮЊPBЕФжаЕуЃЌD1ЮЊPDЕФжаЕуЃЌдђСНИіРтзЖAЉB1CD1 ЃЌ PЉABCDЕФЬхЛ§жЎБШЪЧЃЈ ЃЉ 
A.1ЃК4
B.3ЃК8
C.1ЃК2
D.2ЃК3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЖдЦЖРЇМвЭЅзджїДДвЕИјгшаЁЖюДћПюВЙЬљЃЌУПЛЇДћПюЖюЮЊ![]() ЭђдЊЃЌДћПюЦкЯога
ЭђдЊЃЌДћПюЦкЯога![]() ИідТЁЂ
ИідТЁЂ![]() ИідТЁЂ
ИідТЁЂ![]() ИідТЁЂ
ИідТЁЂ![]() ИідТЁЂ
ИідТЁЂ![]() ИідТЮхжжЃЌетЮхжжДћПюЦкЯоеўИЎЗжБ№ашвЊВЙжњ
ИідТЮхжжЃЌетЮхжжДћПюЦкЯоеўИЎЗжБ№ашвЊВЙжњ![]() дЊЁЂ
дЊЁЂ![]() дЊЁЂ
дЊЁЂ![]() дЊЁЂ
дЊЁЂ![]() дЊЁЂ
дЊЁЂ![]() дЊЃЌДг
дЊЃЌДг![]() ФъЯэЪмДЫЯюеўВпЕФРЇФбЛЇжаГщШЁСЫ
ФъЯэЪмДЫЯюеўВпЕФРЇФбЛЇжаГщШЁСЫ![]() ЛЇНјааСЫЕїВщЭГМЦЃЌбЁШЁДћПюЦкЯоЕФЦЕЪ§ШчЯТБэЃК
ЛЇНјааСЫЕїВщЭГМЦЃЌбЁШЁДћПюЦкЯоЕФЦЕЪ§ШчЯТБэЃК
ДћПюЦкЯо |
|
|
|
|
|
ЦЕЪ§ |
|
|
|
|
|
вдЩЬБъИїжжДћПюЦкЯоЕФЦЕТЪзїЮЊ![]() ФъЦЖРЇМвЭЅбЁдёИїжжДћПюЦкЯоЕФИХТЪ.
ФъЦЖРЇМвЭЅбЁдёИїжжДћПюЦкЯоЕФИХТЪ.
ЃЈ1ЃЉФГаЁЧј![]() ФъЙВга
ФъЙВга![]() ЛЇзМБИЯэЪмДЫЯюеўВпЃЌМЦЫуЦфжаЧЁгаСНЛЇбЁдёДћПюЦкЯоЮЊ
ЛЇзМБИЯэЪмДЫЯюеўВпЃЌМЦЫуЦфжаЧЁгаСНЛЇбЁдёДћПюЦкЯоЮЊ![]() ИідТЕФИХТЪЃЛ
ИідТЕФИХТЪЃЛ
ЃЈ2ЃЉЩшИјЯэЪмДЫЯюеўВпЕФФГРЇФбЛЇВЙЬљЮЊ![]() дЊЃЌаДГі
дЊЃЌаДГі![]() ЕФЗжВМСаЃЌШєдЄМЦ
ЕФЗжВМСаЃЌШєдЄМЦ![]() ФъШЋЪага
ФъШЋЪага![]() ЭђЛЇЯэЪмДЫЯюеўВпЃЌЙРМЦ
ЭђЛЇЯэЪмДЫЯюеўВпЃЌЙРМЦ![]() ФъИУЪаЙВвЊВЙЬљЖрЩйЭђдЊ.
ФъИУЪаЙВвЊВЙЬљЖрЩйЭђдЊ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}ТњзуЃКa1=1ЃЌa2=2ЃЌЧвan+1=2an+3anЉ1ЃЈnЁн2ЃЌnЁЪN+ЃЉЃЎ
ЃЈ1ЃЉЩшbn=an+1+anЃЈnЁЪN+ЃЉЃЌЧѓжЄ{bn}ЪЧЕШБШЪ§СаЃЛ
ЃЈ2ЃЉЃЈiЃЉЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈiiЃЉЧѓжЄЃКЖдгкШЮвтnЁЪN+ЖМга ![]() +
+ ![]() +Ё+
+Ё+ ![]() +
+ ![]() ЃМ
ЃМ ![]() ГЩСЂЃЎ
ГЩСЂЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
(1)Чѓ![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
(2)ШєКЏЪ§![]() ЃЌ
ЃЌ ![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЕФСНИіСуЕуЃЌ
ЕФСНИіСуЕуЃЌ ![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЕФЕМКЏЪ§ЃЌжЄУїЃК
ЕФЕМКЏЪ§ЃЌжЄУїЃК ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЧњЯп
ЃЌЧњЯп![]() дкЕу
дкЕу![]() ДІЕФЧаЯпгыжБЯп
ДІЕФЧаЯпгыжБЯп![]() ДЙжБЃЈЦфжа
ДЙжБЃЈЦфжа![]() ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉЃЎ
ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉЃЎ
ЃЈЂёЃЉЧѓ![]() ЕФНтЮіЪНМАЕЅЕїЕнМѕЧјМфЃЛ
ЕФНтЮіЪНМАЕЅЕїЕнМѕЧјМфЃЛ
ЃЈЂђЃЉШєКЏЪ§![]() ЮоСуЕуЃЌЧѓ
ЮоСуЕуЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com