
【题目】已知{an}是等差数列,Sn是其前n项和.已知a1+a3=16,S4=28.
(1)求数列{an}的通项公式
(2)当n取何值时Sn最大,并求出这个最大值.
【答案】
(1)解:设等差数列{an}的公差为d,
∵a1+a3=16,S4=28.∴2a1+2d=16,4a1+ ![]() d=28,
d=28,
联立解得:a1=10,d=﹣2.
∴an=10﹣2(n﹣1)=12﹣2n.
(2)解:令an=12﹣2n≥0,解得n≤6.
∴n=5,或6时,Sn取得最大值,为S6= ![]() =30.
=30.
【解析】(1)设等差数列{an}的公差为d,利用等差数列的通项公式与求和公式即可得出.(2)令an≥0,解得n≤6.可得n=5,或6时,Sn取得最大值.
【考点精析】本题主要考查了等差数列的通项公式(及其变式)和等差数列的前n项和公式的相关知识点,需要掌握通项公式:![]() 或
或![]() ;前n项和公式:
;前n项和公式:![]() 才能正确解答此题.
才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某餐馆一天中要购买A,B两种蔬菜每斤的价格分别为2元和3元,根据需要,A种蔬菜至少要买6斤,B种蔬菜至少要买4斤,而且一天中购买这两种蔬菜的总费用不能超过60元. 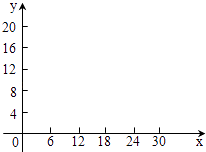
(1)写出一天中A种蔬菜购买的数量x和B种蔬菜购买的数量y之间的不等式组;
(2)在下面给定的坐标系中画出(1)中不等式组表示的平面区域(用阴影表示),并求出它的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,CA=CB,M,N,P分别为AB,A1C1 , BC的中点. 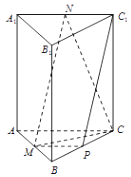
求证:
(1)C1P∥平面MNC;
(2)平面MNC⊥平面ABB1A1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(﹣2,0),N(2,0),动点P满足条件 ![]() .记动点P的轨迹为W.
.记动点P的轨迹为W.
(1)求W的方程;
(2)若A,B是W上的不同两点,O是坐标原点,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解学校食堂的服务情况,随机调查了50名就餐的教师和学生.根据这50名师生对餐厅服务质量进行评分,绘制出了频率分布直方图(如图所示),其中样本数据分组为[40,50),[50,60),…,[90,100]. 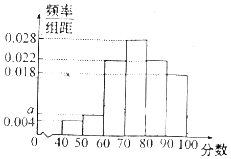
(1)求频率分布直方图中a的值;
(2)从评分在[40,60)的师生中,随机抽取2人,求此人中恰好有1人评分在[40,50)上的概率;
(3)学校规定:师生对食堂服务质量的评分不得低于75分,否则将进行内部整顿,试用组中数据估计该校师生对食堂服务质量评分的平均分,并据此回答食堂是否需要进行内部整顿.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn , 且Sn=n(n+1)(n∈N*)
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:an= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3)令cn= ![]() (n∈N*),求数列{cn}的前n项和Tn .
(n∈N*),求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,满足下列条件的有两个的是( )
A.![]()
B.![]()
C.a=1,b=2,c=3
D.a=3,b=2,A=60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , a1=1,且nan+1=(n+2)Sn , n∈N* .
(1)求证:数列 ![]() 为等比数列;
为等比数列;
(2)求数列{Sn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1 , O是底面ABCD对角线的交点.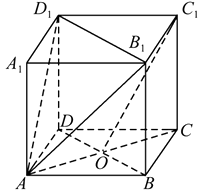
求证:(I) C1O∥面AB1D1;
(II)面A1C⊥面AB1D1 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com