
 如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD,AB距离分别为9m,3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,MN:NE=16:9.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD,AB距离分别为9m,3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,MN:NE=16:9.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).| 3x |
| x-9 |
| 9x2 |
| (x-9)2 |
| 9 |
| 16 |
| 9 |
| 16 |
| 9 |
| 16 |
| 9x2 |
| (x-9)2 |
| 9 |
| 16 |
| 18x(x-9)2-9x2(2x-18) |
| (x-9)4 |
| 9 |
| 8 |
| x[(x-9)3-81] |
| (x-9)3 |
| 3 | 3 |
| 3 | 3 |
| 3 | 3 |
| 3 | 3 |
| 3 | 3 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
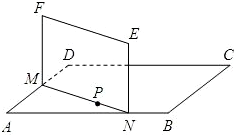
 如图,已知两个正方行ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
如图,已知两个正方行ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 (下列两道题任选做一道,若两道都做,则以第一道计分)
(下列两道题任选做一道,若两道都做,则以第一道计分)查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示为某风景区设计建造的一个休闲广场,广场的中间造型的平面图是由两个相同的矩形ABCD和EFGH构成对称的十字形区域,十字形区域面积为2000m2,计划在正方方形MNPQ上建一座“观景花坛”,造价为每平方4100元,在四个相同的矩形上(图中阴影部分)铺石材地坪,价格为每平方110元,再在四个空角(如△DQH等)上铺草坪,价格为每平方80元.设AD长为xm,DQ长为ym.
如图所示为某风景区设计建造的一个休闲广场,广场的中间造型的平面图是由两个相同的矩形ABCD和EFGH构成对称的十字形区域,十字形区域面积为2000m2,计划在正方方形MNPQ上建一座“观景花坛”,造价为每平方4100元,在四个相同的矩形上(图中阴影部分)铺石材地坪,价格为每平方110元,再在四个空角(如△DQH等)上铺草坪,价格为每平方80元.设AD长为xm,DQ长为ym.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•泉州模拟)如图,在棱长为1的正方体ABCD-A1B1C1D1的对角线AC1上任取一点P,以A为球心,AP为半径作一个球.设AP=x,记该球面与正方体表面的交线的长度和为f(x),则函数f(x)的图象最有可能的是( )
(2013•泉州模拟)如图,在棱长为1的正方体ABCD-A1B1C1D1的对角线AC1上任取一点P,以A为球心,AP为半径作一个球.设AP=x,记该球面与正方体表面的交线的长度和为f(x),则函数f(x)的图象最有可能的是( )查看答案和解析>>
科目:高中数学 来源:2013届贵州省高二上学期期末考试数学 题型:选择题
如图,正方休ABCD—A1B1C1D1中,E、F为AA1、AB的中点,则图中与EF是异面直线的直线有( )条
A.8 B . 9 C .10 D .11

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com