
分析 (1)画出函数图象,利用函数图象的交点问题判断即可.
(2)根据单调性的定义证明,运用图象写出单调区间,结合导数判断即可.
解答 解:(1)∵函数f(x)=|$\frac{1}{x}$-1|.
∴画出函数图象;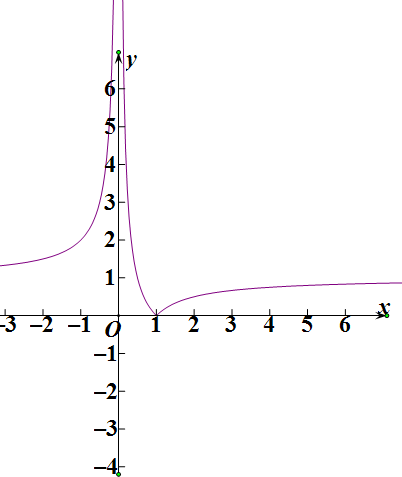
根据图象判断有2个交点,
故函数y=f(x)-3有2个零点;
(2)设任意两个实数x1,x2∈(0,1],且x1<x2,
$\frac{1}{{x}_{1}}$$>\frac{1}{{x}_{2}}$≥1,
∴$\frac{1}{{x}_{1}}$-1$>\frac{1}{{x}_{2}}$-1≥0,
∵函数f(x)=|$\frac{1}{x}$-1|.
∴f(x1)>f(x2)
∴(-∞,0),(1,+∞)单调递增;(0,1)单调递减
(3)根据题意与函数关系式得出;
f(x)与y=mx有2个交点,
根据图象可得出:y=1-$\frac{1}{x}$,x>1,与y=mx有2个交点,
y′=$\frac{1}{{x}^{2}}$,∴$\frac{1}{{x}_{0}^{2}}$=m,x0=$\frac{1}{\sqrt{m}}$,切点为($\frac{1}{\sqrt{m}}$,$\sqrt{m}$)在y=1-$\frac{1}{x}$,x>1的图象上,
∴$\sqrt{m}$=$1-\sqrt{m}$,m=$\frac{1}{4}$,
∴m的范围为:(0,$\frac{1}{4}$)
点评 本题综合考察了函数性质,定义,运用数形结合的思想解决零点问题,属于难度较大的题目.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
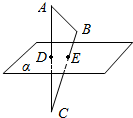 如图所示,D、E分别是△ABC的边AC、BC上的点,平面α经过D、E两点.
如图所示,D、E分别是△ABC的边AC、BC上的点,平面α经过D、E两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x,y,z同号 | B. | y,z同号,且x与它们异号 | ||
| C. | y,z同号,x不能确定 | D. | x,y,z的符号均不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+2y-8=0 | B. | x+2y+8=0 | C. | 2x-y-4=0 | D. | 2x-y+4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 设函数f(x)=|x2-2x|(x∈R).
设函数f(x)=|x2-2x|(x∈R).| x | … | -2 | 0 | 1 | 2 | 3 | … |
| y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com