
设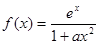 ,其中
,其中
(Ⅰ)当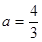 时,求
时,求 的极值点;
的极值点;
(Ⅱ)若 为R上的单调函数,求a的取值范围。
为R上的单调函数,求a的取值范围。
(Ⅰ)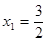 是极小值点,
是极小值点, 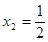 是极大值点(Ⅱ)
是极大值点(Ⅱ)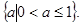
【解析】本试题主要是考查了导数在研究函数中的运用。
(1)对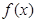 求导得
求导得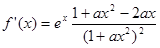 ①
①
(Ⅰ)当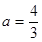 时,若
时,若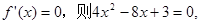
解得 ,判定单调性得到极值。
,判定单调性得到极值。
(2)若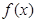 为R上的单调函数,则
为R上的单调函数,则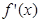 在R上不变号,
在R上不变号,
结合①与条件a>0,知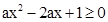 在R上恒成立转化为不等式恒成立问题来求解参数的范围。
在R上恒成立转化为不等式恒成立问题来求解参数的范围。
解:对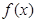 求导得
求导得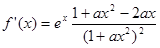 ①……………2分
①……………2分
(Ⅰ)当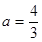 时,若
时,若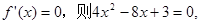
解得 ……………4分
……………4分
综合①,可知
|
|
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
↗ |
极大值 |
↘ |
极小值 |
↗ |
所以, 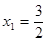 是极小值点,
是极小值点, 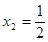 是极大值点. ……………8分
是极大值点. ……………8分
(II)若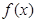 为R上的单调函数,则
为R上的单调函数,则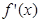 在R上不变号,
在R上不变号,
结合①与条件a>0,知 在R上恒成立,……………10分
在R上恒成立,……………10分
因此 由此并结合
由此并结合 ,知
,知 。
。
所以a的取值范围为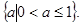 ……………14分
……………14分


科目:高中数学 来源:2012届湖北省鄂州二中高三十一月份阶段性考试理科数学 题型:解答题
(本题满分12分)设函数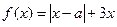 ,其中
,其中 。
。
(Ⅰ)当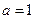 时,求不等式
时,求不等式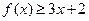 的解集;
的解集;
(Ⅱ)若不等式 的解集为
的解集为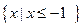 ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省高三(奥班)10月月考理科数学试卷(解析版) 题型:解答题
选修4-5:不等式选讲(本小题满分10分)
设函数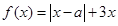 ,其中
,其中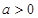 。
。
(Ⅰ)当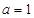 时,求不等式
时,求不等式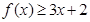 的解集;
的解集;
(Ⅱ)若不等式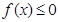 的解集为
的解集为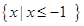 ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年海南省高三第六次月考理科数学试卷(解析版) 题型:解答题
设函数 ,其中
,其中 。
。
(Ⅰ)当 时,求不等式
时,求不等式 的解集
的解集
(Ⅱ)若不等式 的解集为
的解集为 ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年新人教版高三一轮复习单元测试(8)数学试卷 题型:解答题
(12分)(理)设函数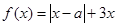 ,其中
,其中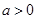 。
。
(Ⅰ)当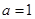 时,求不等式
时,求不等式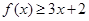 的解集;
的解集;
(Ⅱ)若不等式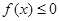 的解集为
的解集为 ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中数学 来源:2011年高考试题数学(全国卷新课标)解析版 题型:解答题
选修4-5:不等式选讲
设函数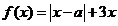 ,其中
,其中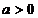 。
。
(Ⅰ)当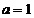 时,求不等式
时,求不等式 的解集;
的解集;
(Ⅱ)若不等式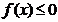 的解集为
的解集为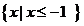 ,求a的值。
,求a的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com