选修4-5:不等式选讲已知函数f(x)=|x+1|+|x-2|,不等式t≤f(x)在R上恒成立.
(Ⅰ)求t的取值范围;
(Ⅱ)记t的最大值为T,若正实数a,bc满足a2+b2+c2=T,求a+2b+c的最大值.
解:(Ⅰ)∵f(x)=|x+1|+|x-2|≥|(x+1)-(x-2)|=3,∴f(x)
min=3.…(2分)∵不等式t≤f(x)在R上恒成立,∴t≤f(x)
min=3,t的取值范围为(-∞,3].…(3分)
(Ⅱ)由(Ⅰ)得T=t
max=3,
由柯西不等式得:(a+2b+c)
2≤(1
2+2
2+1
2)(a
2+b
2+c
2)=18,∴
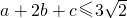
.…(5分)
当且仅当
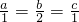
即
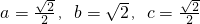
时,a+2b+c的最大值为

.…(7分)
分析:(Ⅰ)利用绝对值三角不等式求出f(x)的最小值,再结合不等式t≤f(x)在R上恒成立即可求得t的取值范围;
(Ⅱ)由(Ⅰ)得T=t
max=3,由柯西不等式得:(a+2b+c)
2≤(1
2+2
2+1
2)(a
2+b
2+c
2)=18即可得到a+2b+c的最大值.
点评:本题主要考查利用绝对值不等式的基本性质求解和证明不等式等基础知识,考查运算求解能力,考查化归与转化思想.

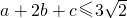 .…(5分)
.…(5分)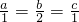 即
即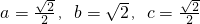 时,a+2b+c的最大值为
时,a+2b+c的最大值为 .…(7分)
.…(7分)
