
【题目】某厂加工的零件按箱出厂,每箱有10个零件,在出厂之前需要对每箱的零件作检验,人工检验方法如下:先从每箱的零件中随机抽取4个零件,若抽取的零件都是正品或都是次品,则停止检验;若抽取的零件至少有1个至多有3个次品,则对剩下的6个零件逐一检验.已知每个零件检验合格的概率为0.8,每个零件是否检验合格相互独立,且每个零件的人工检验费为2元.
(1)设1箱零件人工检验总费用为![]() 元,求
元,求![]() 的分布列;
的分布列;
(2)除了人工检验方法外还有机器检验方法,机器检验需要对每箱的每个零件作检验,每个零件的检验费为1.6元.现有1000箱零件需要检验,以检验总费用的数学期望为依据,在人工检验与机器检验中,应该选择哪一个?说明你的理由.
【答案】(1)详见解析(2)应该选择人工检验,详见解析
【解析】
(1)根据题意,工人抽查的4个零件中,分别计算出4个都是正品或者都是次品,4个不全是次品的人工费用,得出![]() 的可能值,利用二项分布分别求出概率,即可列出
的可能值,利用二项分布分别求出概率,即可列出![]() 的分布列;
的分布列;
(2)由(1)求出![]() 的数学期望
的数学期望![]() ,根据条件分别算出1000箱零件的人工检验和机器检验总费用的数学期望,比较即可得出结论.
,根据条件分别算出1000箱零件的人工检验和机器检验总费用的数学期望,比较即可得出结论.
解:(1)由题可知,工人抽查的4个零件中,
当4个都是正品或者都是次品,则人工检验总费用为:![]() 元,
元,
当4个不全是次品时,人工检验总费用都为:![]() 元,
元,
所以![]() 的可能取值为8,20,
的可能取值为8,20,
![]() ,
,
![]() ,
,
则![]() 的分布列为
的分布列为
| 8 | 20 |
| 0.4112 | 0.5888 |
(2)由(1)知,![]() ,
,
所以1000箱零件的人工检验总费用的数学期望为![]() 元,
元,
因为1000箱零件的机器检验总费用的数学期望为![]() 元,
元,
且![]() ,
,
所以应该选择人工检验.


科目:高中数学 来源: 题型:
【题目】已知直线![]() 过抛物线
过抛物线![]() 的焦点,且与该抛物线交于
的焦点,且与该抛物线交于![]() ,
,![]() 两点,若线段
两点,若线段![]() 的长是16,
的长是16,![]() 的中点到
的中点到![]() 轴的距离是6,
轴的距离是6,![]() 是坐标原点,则( ).
是坐标原点,则( ).
A.抛物线![]() 的方程是
的方程是![]() B.抛物线的准线方程是
B.抛物线的准线方程是![]()
C.直线![]() 的方程是
的方程是![]() D.
D.![]() 的面积是
的面积是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数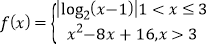 若方程f(x)=m有4个不同的实根x1,x2,x3,x4,且x1<x2<x3<x4,则(
若方程f(x)=m有4个不同的实根x1,x2,x3,x4,且x1<x2<x3<x4,则(![]() )(x3+x4)=( )
)(x3+x4)=( )
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱![]() 中,侧面
中,侧面![]() 为菱形,
为菱形,![]() ,
,![]() ,侧面
,侧面![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .点
.点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
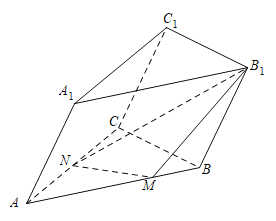
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解运动健身减肥的效果,某健身房调查了20名肥胖者,测量了他们的体重(单位:千克).健身之前他们的体重情况如三维饼图(1)所示,经过半年的健身后,他们的体重情况如三维饼图(2)所示,对比健身前后,关于这20名肥胖者,下面结论正确的是( )
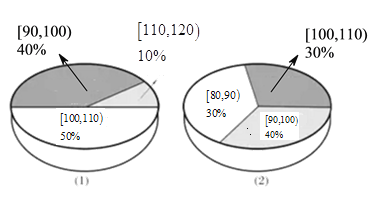
A.他们健身后,体重在区间![]() 内的人数不变
内的人数不变
B.他们健身后,体重在区间![]() 内的人数减少了2个
内的人数减少了2个
C.他们健身后,体重在区间![]() 内的肥胖者体重都有减轻
内的肥胖者体重都有减轻
D.他们健身后,这20位肥胖着的体重的中位数位于区间![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的3月12日是植树节,某公司为了动员职工积极参加植树造林,在植树节期间开展植树有奖活动,设有甲、乙两个摸奖箱,每位植树者植树每满30棵获得一次甲箱内摸奖机会,植树每满50棵获得一次乙箱内摸奖机会,每箱内各有10个球(这些球除颜色外全相同),甲箱内有红、黄、黑三种颜色的球,其中![]() 个红球,
个红球,![]() 个黄球,5个黑球,乙箱内有4个红球和6个黄球,每次摸一个球后放回原箱,摸得红球奖100元,黄球奖50元,摸得黑球则没有奖金.
个黄球,5个黑球,乙箱内有4个红球和6个黄球,每次摸一个球后放回原箱,摸得红球奖100元,黄球奖50元,摸得黑球则没有奖金.
(1)经统计,每人的植树棵数![]() 服从正态分布
服从正态分布![]() ,若其中有200位植树者参与了抽奖,请估计植树的棵数
,若其中有200位植树者参与了抽奖,请估计植树的棵数![]() 在区间
在区间![]() 内并中奖的人数(结果四舍五入取整数);
内并中奖的人数(结果四舍五入取整数);
附:若![]() ,则
,则![]() ,
,
![]() .
.
(2)若![]() ,某位植树者获得两次甲箱内摸奖机会,求中奖金额
,某位植树者获得两次甲箱内摸奖机会,求中奖金额![]() (单位:元)的分布列;
(单位:元)的分布列;
(3)某人植树100棵,有两种摸奖方法,
方法一:三次甲箱内摸奖机会;
方法二:两次乙箱内摸奖机会;
请问:这位植树者选哪一种方法所得奖金的期望值较大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司准备设计一个精美的心形巧克力盒子,它是由半圆![]() 、半圆
、半圆![]() 和正方形ABCD组成的,且
和正方形ABCD组成的,且![]() .设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,
.设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,![]() ,矩形EFGH的面积为
,矩形EFGH的面积为![]() .
.
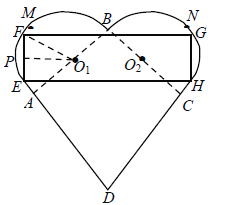
(1)写出S关于![]() 的函数关系式
的函数关系式![]()
(2)当![]() 为何值时矩形EFGH的面积最大?
为何值时矩形EFGH的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是某高架桥箱梁的横截面,它由上部路面和下部支撑箱两部分组成.如图2,路面宽度![]() ,下部支撑箱CDEF为等腰梯形(
,下部支撑箱CDEF为等腰梯形(![]() ),且
),且![]() .为了保证承重能力与稳定性,需下部支撑箱的面积为
.为了保证承重能力与稳定性,需下部支撑箱的面积为![]() ,高度为2m且
,高度为2m且![]() ,若路面AB.侧边CF和DE,底部EF的造价分别为4a千元/m,5a千元/m,6a千元/m(a为正常数),
,若路面AB.侧边CF和DE,底部EF的造价分别为4a千元/m,5a千元/m,6a千元/m(a为正常数),![]() .
.

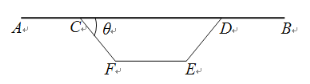
(1)试用θ表示箱梁的总造价y(千元);
(2)试确定cosθ的值,使总造价最低?并求最低总造价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com