
【题目】函数①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中对于
;其中对于![]() 定义域内任意一个自变量
定义域内任意一个自变量![]() 都存在唯一自变量
都存在唯一自变量![]() ,使得
,使得![]() 成立的函数是()
成立的函数是()
A.①③B.②③C.①②④D.③
【答案】D
【解析】
根据题意可知其中对于f(x)定义域内的任意一个自变量x1都存在唯一个自变量x2,使![]() 3即要判断对于任意一个自变量x,即函数在定义域内每个函数值,都有其倒数的9倍,从而得到结论.
3即要判断对于任意一个自变量x,即函数在定义域内每个函数值,都有其倒数的9倍,从而得到结论.
在①f(x)=3lnx中,∵f(1)=0,∴不存在自变量![]() ,使
,使![]() 成立,故①不成立;
成立,故①不成立;
在②f(x)=3ecosx中,∵函数不是单调函数,
∴对于定义域内的任意一个自变量![]() ,使
,使![]() 成立的自变量
成立的自变量![]() 不唯一,故②不成立;
不唯一,故②不成立;
在③![]() 中,函数是单调函数,且函数值不为0,
中,函数是单调函数,且函数值不为0,
故定义域内的任意一个自变量![]() 都存在唯一一个自变量
都存在唯一一个自变量![]() ,使
,使![]() 成立,故③成立;
成立,故③成立;
在④f(x)=3cosx中,∵f(![]() )=0,∴不存在自变量
)=0,∴不存在自变量![]() ,使
,使![]() 成立,故④不成立。
成立,故④不成立。
故选:D.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() ,如果存在常数p,使得对任意正整数n,总有
,如果存在常数p,使得对任意正整数n,总有![]() 成立,那么我们称数列
成立,那么我们称数列![]() 为“p-摆动数列”.
为“p-摆动数列”.
(Ⅰ)设![]() ,
,![]() ,
,![]() ,判断
,判断![]() 、
、![]() 是否为“p-摆动数列”,并说明理由;
是否为“p-摆动数列”,并说明理由;
(Ⅱ)已知“p-摆动数列”![]() 满足
满足![]() ,
,![]() ,求常数p的值;
,求常数p的值;
(Ⅲ)设![]() ,且数列
,且数列![]() 的前n项和为
的前n项和为![]() ,求证:数列
,求证:数列![]() 是“p-摆动数列”,并求出常数p的取值范围.
是“p-摆动数列”,并求出常数p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具公司生产甲、乙两种书柜,制柜需先制白胚再油漆,每种柜的制造白胚工时数、油漆工时数的有关数据如下:
工艺要求 | 产品甲 | 产品乙 | 生产能力(工时/天) |
制白胚工时数 | 6 | 12 | 120 |
油漆工时数 | 8 | 4 | 64 |
单位利润 | 20元 | 24元 |
则该公司合理安排这两种产品的生产,每天可获得的最大利润为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划销售某种食品,现邀请甲、乙两个商家进场试销10天.两个商家向超市提供的日返利方案如下:甲商家每天固定返利60元,且每卖出一件食品商家再返利3元;乙商家无固定返利,卖出不超出30件(含30件)的食品,每件食品商家返利5元,超出30件的部分每件返利10元. 经统计,试销这10天两个商家每天的销量如图所示的茎叶图(茎为十位数字,叶为个位数字):
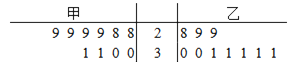
(1)现从甲商家试销的10天中随机抽取两天,求这两天的销售量都小于30件的概率;
(2)根据试销10天的数据,将频率视作概率,用样本估计总体,回答以下问题:
①记商家乙的日返利额为X(单位:元),求X的分布列和数学期望;
②超市拟在甲、乙两个商家中选择一家长期销售,如果仅从日返利额的数学期望考虑,请利用所学的统计学知识为超市作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
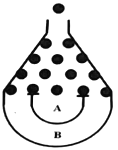
【题目】某超市国庆大酬宾,购物满100元可参加一次游戏抽奖活动,游戏抽奖规则如下:顾客将一个半径适当的小球放入如图所示的容器正上方的入口处,小球自由落下过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,落入A袋得奖金4元,落入B袋得奖金8元,已知小球每次遇到黑色障碍物时,向左向右下落的概率都为![]() .已知李女士当天在该超市购物消费128元,按照活动要求,李女士的活动奖金期望值为_____元.
.已知李女士当天在该超市购物消费128元,按照活动要求,李女士的活动奖金期望值为_____元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;
”;
②“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③![]() 命题“,使得
命题“,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”;
”;
④命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
其中所有正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①![]() 越小,X与Y有关联的可信度越小;②若两个随机变量的线性相关性越强,则相关系数r的值越接近于1;③“若
越小,X与Y有关联的可信度越小;②若两个随机变量的线性相关性越强,则相关系数r的值越接近于1;③“若![]() ,则
,则![]() 类比推出,“若
类比推出,“若![]() ,则
,则![]() ;④命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是使用了“三段论”,推理形式错误.其中说法正确的有( )个
;④命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是使用了“三段论”,推理形式错误.其中说法正确的有( )个
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com