
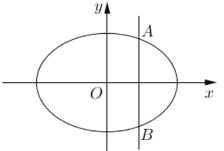
【题目】已知直线![]()
![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,其中
两点,其中![]() 在第一象限,
在第一象限,![]() 是椭圆上一点.
是椭圆上一点.
(1)记![]() 、
、![]() 是椭圆
是椭圆![]() 的左右焦点,若直线
的左右焦点,若直线![]() 过
过![]() ,当
,当![]() 到
到![]() 的距离与到直线
的距离与到直线![]() 的距离相等时,求点
的距离相等时,求点![]() 的横坐标;
的横坐标;
(2)若点![]() 关于
关于![]() 轴对称,当
轴对称,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程;
的方程;
(3)设直线![]() 和
和![]() 与
与![]() 轴分别交于
轴分别交于![]() ,证明:
,证明:![]() 为定值.
为定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)由题意可得焦点![]() ,
,![]() 的坐标,进而可求出
的坐标,进而可求出![]() 的坐标,设
的坐标,设![]() 的坐标,注意横坐标的范围
的坐标,注意横坐标的范围![]() ,在椭圆上,又
,在椭圆上,又![]() 到
到![]() 的距离与到直线
的距离与到直线![]() 的距离相等,可求出
的距离相等,可求出![]() 的横坐标;
的横坐标;
(2)![]() ,
,![]() ,
,![]() 个点的位置关系,可设一个点坐标,写出其他两点的坐标,写出面积的表达式,根据均值不等式可求出横纵坐标的关系,又在椭圆上,进而求出具体的坐标,再求直线
个点的位置关系,可设一个点坐标,写出其他两点的坐标,写出面积的表达式,根据均值不等式可求出横纵坐标的关系,又在椭圆上,进而求出具体的坐标,再求直线![]() 的方程;
的方程;
(3)设![]() ,
,![]() 的坐标,得出直线
的坐标,得出直线![]() ,
,![]() 的方程,进而求出两条直线与
的方程,进而求出两条直线与![]() 轴的交点坐标,用
轴的交点坐标,用![]() ,
,![]() 的坐标表示,而
的坐标表示,而![]() ,
,![]() 又在椭圆上,进而求出结果.
又在椭圆上,进而求出结果.
(1)设![]() ,依题意得,
,依题意得,![]() ,联立椭圆方程:
,联立椭圆方程:![]() ,把
,把![]() 代入得:
代入得:
![]() ,
,![]() ;
;
又因为![]() ,代入得:
,代入得:![]() ;
;
(2)设![]() ,则
,则![]() ,则
,则![]() ,
,
又因为![]() 在椭圆
在椭圆![]() 上,
上,
所以![]() ,
,
![]()
![]()
则![]() ,当且仅当
,当且仅当![]() 时,取等号,即
时,取等号,即![]() ,则
,则![]() ,所以
,所以![]() ;
;
(3)设![]() ,
,
则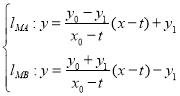
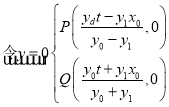 ,
,
则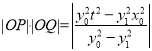 ,又因为
,又因为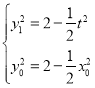 ,代入得:
,代入得: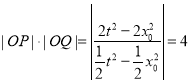 ,故为定值.
,故为定值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 截直线
截直线![]() 所得的线段的长度为
所得的线段的长度为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上的点,
上的点,![]() 是坐标原点,若
是坐标原点,若![]() ,判定四边形
,判定四边形![]() 的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 的参数方程为
的参数方程为 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到![]() 距离的最大值及该点坐标.
距离的最大值及该点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,且满足以线段
两点,且满足以线段![]() 为直径的圆,圆心为
为直径的圆,圆心为![]() ,且过坐标原点
,且过坐标原点![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若圆![]() 过点
过点![]() ,求直线
,求直线![]() 的方程和圆
的方程和圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应“生产发展、生活富裕、乡风文明、村容整洁、管理民主”的社会主义新农村建设,某自然村将村边一块废弃的扇形荒地(如图)租给蜂农养蜂、产蜜与售蜜.已知扇形AOB中,![]() ,
,![]() (百米),荒地内规划修建两条直路AB,OC,其中点C在
(百米),荒地内规划修建两条直路AB,OC,其中点C在![]() 上(C与A,B不重合),在小路AB与OC的交点D处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区.设
上(C与A,B不重合),在小路AB与OC的交点D处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区.设![]() ,蜂巢区的面积为S(平方百米).
,蜂巢区的面积为S(平方百米).
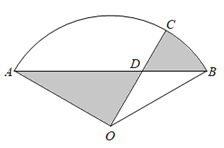
(1)求S关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为何值时,蜂巢区的面积S最小,并求此时S的最小值.
为何值时,蜂巢区的面积S最小,并求此时S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家每年都会对中小学生进行体质健康监测,一分钟跳绳是监测的项目之一.今年某小学对本校六年级300名学生的一分钟跳绳情况做了统计,发现一分钟跳绳个数最低为10,最高为189.现将跳绳个数分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 6组,并绘制出如下的频率分布直方图.
6组,并绘制出如下的频率分布直方图.
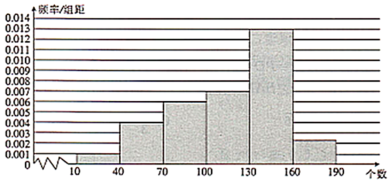
(1)若一分钟跳绳个数达到160为优秀,求该校六年级学生一分钟跳绳为优秀的人数;
(2)上级部门要对该校体质监测情况进行复查,发现每组男、女学生人数比例有很大差别,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() .试估计此校六年级男生一分钟跳绳个数的平均数(同一组中的数据用该组区间的中点值作代表,结果保留整数).
.试估计此校六年级男生一分钟跳绳个数的平均数(同一组中的数据用该组区间的中点值作代表,结果保留整数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上顶点为A,右焦点为F,O是坐标原点,
的上顶点为A,右焦点为F,O是坐标原点,![]() 是等腰直角三角形,且周长为
是等腰直角三角形,且周长为![]() .
.
(1)求椭圆的方程;
(2)若直线l与AF垂直,且交椭圆于B,C两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是( )
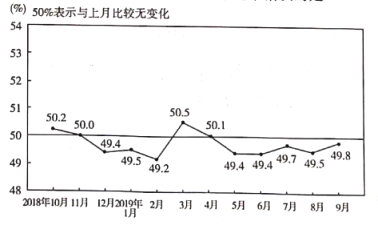
A.12个月的PMI值不低于50%的频率为![]()
B.12个月的PMI值的平均值低于50%
C.12个月的PMI值的众数为49.4%
D.12个月的PMI值的中位数为50.3%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为![]() .
.
(1)问该厂至少有多少名维修工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不小于![]() ?
?
(2)已知1名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,能使该厂产生5万元的利润,否则将不产生利润.若该厂现有2名工人,求该厂每月获利的均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com