
【题目】定义在![]() 的函数
的函数![]() 的导函数为
的导函数为![]() .
.
证明:(1)![]() 在区间
在区间![]() 存在唯一极小值点;
存在唯一极小值点;
(2)![]() 有且仅有2个零点.
有且仅有2个零点.
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】国际羽毛球比赛规则从2006年5月开始,正式决定实行21分的比赛规则和每球得分制,并且每次得分者发球,所有单项的每局获胜分至少是21分,最高不超过30分,即先到21分的获胜一方赢得该局比赛,如果双方比分为![]() 时,获胜的一方需超过对方2分才算取胜,直至双方比分打成
时,获胜的一方需超过对方2分才算取胜,直至双方比分打成![]() 时,那么先到第30分的一方获胜.在一局比赛中,甲发球赢球的概率为
时,那么先到第30分的一方获胜.在一局比赛中,甲发球赢球的概率为![]() ,甲接发球贏球的概率为
,甲接发球贏球的概率为![]() ,则在比分为
,则在比分为![]() ,且甲发球的情况下,甲以
,且甲发球的情况下,甲以![]() 赢下比赛的概率为( )
赢下比赛的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,且
,且![]() 对一切
对一切![]() 都成立.
都成立.
(1)当![]() 时.
时.
①求数列![]() 的通项公式;
的通项公式;
②若![]() ,求数列
,求数列![]() 的前
的前![]() 项的和
项的和![]() ;
;
(2)是否存在实数![]() ,使数列
,使数列![]() 是等差数列.如果存在,求出
是等差数列.如果存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问某地100名高中学生在选择座位时是否挑同桌,得到如下![]() 列联表:
列联表:
男生 | 女生 | 合计 | |
挑同桌 | 30 | 40 | 70 |
不挑同桌 | 20 | 10 | 30 |
总计 | 50 | 50 | 100 |
(1)从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5名学生中随机选取3名做深度采访,求这3名学生中恰有2名挑同桌的概率;
(2)根据以上![]() 列联表,是否有
列联表,是否有![]() 以上的把握认为“性别与在选择座位时是否挑同桌”有关?
以上的把握认为“性别与在选择座位时是否挑同桌”有关?
下面的临界值表供参考:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(参考公式: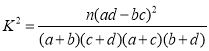 ,其中
,其中.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是中国成立70周年,也是全面建成小康社会的关键之年.为了迎祖国70周年生日,全民齐心奋力建设小康社会,某校特举办“喜迎国庆,共建小康”知识竞赛活动.下面的茎叶图是参赛两组选手答题得分情况,则下列说法正确的是( )
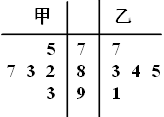
A.甲组选手得分的平均数小于乙组选手的平均数B.甲组选手得分的中位数大于乙组选手的中位数
C.甲组选手得分的中位数等于乙组选手的中位数D.甲组选手得分的方差大于乙组选手的的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型公司为了切实保障员工的健康安全,贯彻好卫生防疫工作的相关要求,决定在全公司范围内举行一次乙肝普查.为此需要抽验960人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.
方案①:将每个人的血分别化验,这时需要验960次.
方案②:按![]() 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组![]() 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这![]() 个人的血就只需检验一次(这时认为每个人的血化验一次);否则,若呈阳性,则需对这
个人的血就只需检验一次(这时认为每个人的血化验一次);否则,若呈阳性,则需对这![]() 个人的血样再分别进行一次化验.这样,该组
个人的血样再分别进行一次化验.这样,该组![]() 个人的血总共需要化验
个人的血总共需要化验![]() 次.
次.
假设此次普查中每个人的血样化验呈阳性的概率为![]() ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案②中,某组![]() 个人中每个人的血化验次数为
个人中每个人的血化验次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)设![]() .试比较方案②中,
.试比较方案②中,![]() 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数).
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com