
【题目】已知![]() ,n∈N*.
,n∈N*.
(1)设f(x)=a0+a1x+a2x2+…+anxn,
①求a0+a1+a2+…+an;
②若在a0,a1,a2,…,an中,唯一的最大的数是a4,试求n的值;
(2)设f(x)=b0+b1(x+1)+b2(x+1)2+…+bn(x+1)n,求![]() .
.
【答案】(1)①![]() ;②n=12或13;(2)
;②n=12或13;(2)![]() (2n+1﹣2﹣n)
(2n+1﹣2﹣n)
【解析】
(1)①可令x=1,代入计算可得所求和;②可得f(x)=(x+2)n=(2+x)n的通项公式,ar最大即为ar≥ar﹣1,且ar≥ar+1,化简计算,结合不等式的解,可得所求值;
(2)由f(x)=[1+(x+1)]n,可得br=C![]() ,r=0,1,…,n,推得
,r=0,1,…,n,推得![]() ,再由二项式定理,计算可得所求和.
,再由二项式定理,计算可得所求和.
解:(1)①由(x+2)n=a0+a1x+a2x2+…+anxn,
可令x=1,可得3n=a0+a1+a2+…+an,
即a0+a1+a2+…+an=3n;
②f(x)=(x+2)n=(2+x)n,
可得ar![]() 2n﹣rxr,r=0,1,…,n,
2n﹣rxr,r=0,1,…,n,
若在a0,a1,a2,…,an中,ar最大,
可得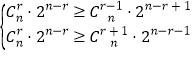 ,即为
,即为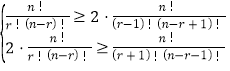 ,
,
化为![]() ,由于r=4时为a4唯一的最大值,
,由于r=4时为a4唯一的最大值,
可得n=12,13;
(2)由f(x)=b0+b1(x+1)+b2(x+1)2+…+bn(x+1)n,
且f(x)=[1+(x+1)]n,可得br=C![]() ,r=0,1,…,n,
,r=0,1,…,n,
则![]() ,
,
由![]()
![]()
![]() ,
,
则![]() (C
(C![]() )
)![]() (2n+1﹣2﹣n).
(2n+1﹣2﹣n).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】![]() 指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当
指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当![]() 数值大于或等于20.5时,我们说体重较重,当
数值大于或等于20.5时,我们说体重较重,当![]() 数值小于20.5时,我们说体重较轻,身高大于或等于
数值小于20.5时,我们说体重较轻,身高大于或等于![]() 我们说身高较高,身高小于170cm我们说身高较矮.
我们说身高较高,身高小于170cm我们说身高较矮.
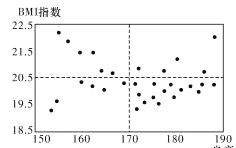
(1)已知某高中共有32名男体育特长生,其身高与![]() 指数的数据如散点图,请根据所得信息,完成下述列联表,并判断是否有
指数的数据如散点图,请根据所得信息,完成下述列联表,并判断是否有![]() 的把握认为男生的身高对
的把握认为男生的身高对![]() 指数有影响.
指数有影响.
身高较矮 | 身高较高 | 合计 | |
体重较轻 | |||
体重较重 | |||
合计 |
(2)①从上述32名男体育特长生中随机选取8名,其身高和体重的数据如表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根据最小二乘法的思想与公式求得线性回归方程为![]() .利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献值(保留两位有效数字)
.利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献值(保留两位有效数字)![]() ;
;
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
残差 | 0.1 | 0.3 | 0.9 |
|
|
②通过残差分析,对于残差的最大(绝对值)的那组数据,需要确认在样本点的采集中是否有人为的错误,已知通过重新采集发现,该组数据的体重应该为![]() .请重新根据最最小二乘法的思想与公式,求出男体育特长生的身高与体重的线性回归方程.
.请重新根据最最小二乘法的思想与公式,求出男体育特长生的身高与体重的线性回归方程.
(参考公式)
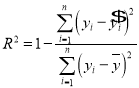 ,
,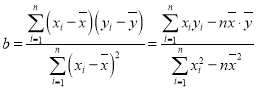 ,
,![]() ,
,![]() ,
,![]() .
.
(参考数据)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
0.10
0.05
0.01
0.005
![]()
2.706
3.811
6.635
7.879
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将高二(1)班的四个同学分到语文、数学、英语三个兴趣小组,每个兴趣小组至少有一名同学的分配方法有多少种?下列结论正确的有( )
A.![]() B.
B.![]()
C.![]() D.18
D.18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面积S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图放置的边长为1的正方形![]() 沿
沿![]() 轴滚动,点
轴滚动,点![]() 恰好经过原点.设顶点
恰好经过原点.设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 有下列判断:①函数
有下列判断:①函数![]() 是偶函数;②对任意的
是偶函数;②对任意的![]() ,都有
,都有![]() ;③函数
;③函数![]() 在区间
在区间![]() 上单调递减;④函数
上单调递减;④函数![]() 的值域是
的值域是![]() ;⑤
;⑤![]() .其中判断正确的序号是__________.
.其中判断正确的序号是__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】指出下列命题是全称量词命题还是存在量词命题,并判断它们的真假.
(1)x∈N,2x+1是奇数;
(2)存在一个x∈R,使![]() =0;
=0;
(3)对任意实数a,|a|>0;
(4)有一个角α,使sinα=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学志愿者协会有6名男同学,4名女同学,在这10名同学中,3名同学来自数学学院,其余7名同学来自物理﹑化学等其他互不相同的七个学院,现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(1)求选出的3名同学是来自互不相同学院的概率;
(2)设![]() 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com