
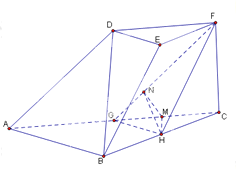
【题目】如图,在三棱台![]() 中,
中,![]() 分别为
分别为![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]()
![]() 平面
平面![]() ,
, ![]() 求平面
求平面![]() 与平面
与平面![]() 所成的角(锐角)的大小.
所成的角(锐角)的大小.
【答案】
(1)
证法一:连接DG,CO,设CD∩GF=O,连接OH
在三棱台DEF-ABC中,
AB=2DE,G为AC的中点
可得DF∥GC,DF=GC
所以四边形DFCG为平行四边形
则0为CD的中点,又H为BC的中点
所以OH∥BD
又![]() 平面
平面![]()
![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
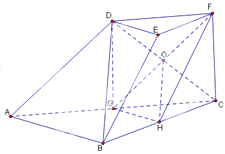
证法二
在三棱台DEF-ABC中,
由BC=2EF,H为BC的中点
可得BH∥EF,BH = EF ,
所以四边形BHEE为平行四边形
可得BE∥HF;
在△ABC中,G为AC的中点,H为BC的中点,
所以GH ∥AB
又GH∩HF=H,所以平面FGH∥平面.ABED
因为BD![]() 平面ABED
平面ABED
所以BD∥平面FGH
(2)解:解法一:
设AB=2,则CF=1
在三棱台DEF-ABC中,
G为AC的中点
由![]()
可得四边形DGCF为平行四边形,
DG ∥CF
C⊥平面ABC
所以DG⊥平面ABC
在△ABC中,由AB⊥BC,![]() ,G是AC中点,
,G是AC中点,
所以.A B = BC. GB⊥GC
因此GB,GC,GD两两垂直,
以G为坐标原点,建立如图所示的空间直角坐标系G—xyz
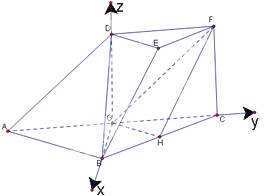
所以![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
可得![]()
![]() ,
,![]()
![]()
故![]() =
=![]() ,
,![]()
![]()
设![]()
![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则
由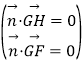 得
得![]()
可得平面![]() 的一个法向量
的一个法向量![]()
![]()
应为![]() 是平面
是平面![]() 的一个法向量
的一个法向量![]() =
=![]() ,
,
所以COS<![]() ,
,![]() >
>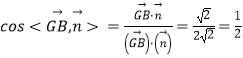
所以平面与平面所成的解锐角的大小为![]()
解法二
作HM⊥AC于点M,作MN⊥GF于点N,连接NM
由FC⊥平面ABC,得HM⊥FC![]()
所以HM⊥平面ACFD
所以∠MNH即为所求的角
在△BGC中,MH∥BG, MH二![]() ,
,
由![]()
可得![]()
从而![]()
由![]() 平面
平面![]() ,
,![]() 平面
平面![]()
得![]()
因此![]()
所以![]()
所以平面FGH平面ACFD所成角(锐角)的大小为![]()
【解析】(1)思路一:连接DG,CD,设CD∩GF=O,连接OH,先证明OH∥BD,从而由直线平面平行的判定定理得BD∥平面HDF;
思路二:先证明平面FGH∥平面ABED,再由平面与平面平行的定义得到BD∥平面HDF。
(2)思路一:连接DG,CD,设CD∩GF=O,连接OH,证明GB,GC,GD两两垂直,以G为坐标原点建立如图所示的空间直角坐标系G-xyz,利用空量向量的夹角公式求解;
思路二:作HM⊥AC于点M,作MN⊥GF于点N,连接NM,证明∠MNH即为所求的角,然后在三角形中求解,
本题涉及到了立体几何中的线面平行与垂直的判定与性质,全面考查立几何中的证明与求解,意在考查学生的空间想象能力和逻辑推理能力;利用空间向量解决立体几何问题是一种成熟的方法,要注意建立适当的空间直角坐标系以及运算的准确性.![]()
【考点精析】解答此题的关键在于理解用空间向量求直线与平面的夹角的相关知识,掌握设直线![]() 的方向向量为
的方向向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,直线与平面所成的角为
,直线与平面所成的角为![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() , 则
, 则![]() 为
为![]() 的余角或
的余角或![]() 的补角的余角.即有:
的补角的余角.即有: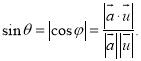 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(2015·陕西)在直角坐标系xOy中,直线l的参数方程为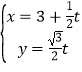 (t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,
(t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,![]() c的极坐标方程为
c的极坐标方程为![]() =2
=2![]() sin
sin![]() .
.
(1)写出![]() c的直角坐标方程;
c的直角坐标方程;
(2)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
x |
|
| |||
| 0 | 5 | -5 | 0 |
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数![]() 的解析式;
的解析式;
(Ⅱ)将![]() 图象上所有点向左平行移动
图象上所有点向左平行移动![]() 个单位长度,得到
个单位长度,得到![]() 的图象. 若
的图象. 若![]() 图象的一个对称中心为
图象的一个对称中心为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足:①对任意x∈(0,+∞),恒有f(2x)=2f(x)成立;②当x∈(1,2]时,f(x)=2﹣x.若f(a)=f(2020),则满足条件的最小的正实数a的值为( )
A. 28 B. 100 C. 34 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
(I)估计顾客同时购买乙和丙的概率;
(II)估计顾客在甲、乙、丙、丁中同时购买3中商品的概率;
(III)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() 且点
且点![]() 和
和![]() 分别为
分别为![]() 和
和![]() 的中点
的中点
(1)求证:![]() 平面
平面![]()
(2)求二面角![]() 的正弦值
的正弦值
(3)设![]() 为棱
为棱![]() 上的点,若直线
上的点,若直线![]() 和平面
和平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长
的长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号t | 1 | 2 | 3 | 4 | 5 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
(1)求y关于t的回归方程![]()
(2)用所求回归方程预测该地区2015年(![]() )的人民币储蓄存款.
)的人民币储蓄存款.
附:回归方程![]() 中
中
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已成椭圆 ![]() 的左右顶点分别为
的左右顶点分别为 ![]() ,上下顶点分别为
,上下顶点分别为 ![]() ,左右焦点分别为
,左右焦点分别为 ![]() ,其中长轴长为4,且圆
,其中长轴长为4,且圆 ![]() 为菱形
为菱形 ![]() 的内切圆.
的内切圆.
(1)求椭圆 ![]() 的方程;
的方程;
(2)点 ![]() 为
为 ![]() 轴正半轴上一点,过点
轴正半轴上一点,过点 ![]() 作椭圆
作椭圆 ![]() 的切线
的切线 ![]() ,记右焦点
,记右焦点 ![]() 在
在 ![]() 上的射影为
上的射影为 ![]() ,若
,若 ![]() 的面积不小于
的面积不小于 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com