
一个路口的红绿灯,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为
40秒,当你到达路口时看见下列三种情况的概率各是多少?
(1) 红灯 (2) 黄灯 (3) 不是红灯
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
一个不透明的袋子中装有4个形状相同的小球,分别标有不同的数字2,3,4, ,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表
,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表
| 摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为7”出现的频数 | 1 | 9 | 14 | 24 | 26 | 37 | 58 | 82 | 109 | 150 |
| “和为7”出现的频率 | 0.10 | 0.45 | 0.47 | 0.40 | 0.29 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
 )
) 的值;
的值;  元,求
元,求 的数学期望和方差。
的数学期望和方差。查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一场娱乐晚会上, 有5位民间歌手(1至5号)登台演唱, 由现场数百名观众投票选出最受欢迎歌手. 各位观众须彼此独立地在选票上选3名选手, 其中观众甲是1号歌手的歌迷, 他必选1号, 不选2号, 另在3至5号中随机选2名. 观众乙和丙对5位歌手的演唱没有偏爱, 因此在1至5号中随机选3名歌手.
(Ⅰ) 求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(Ⅱ) X表示3号歌手得到观众甲、乙、丙的票数之和, 求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
近几年来,我国许多地区经常出现干旱现象,为抗旱经常要进行人工降雨。现由天气预报得知,某地在未来3天的指定时间的降雨概率是:前2天均为50%,后1天为80%.3天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.求不需要人工降雨的天数x的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
“肇实,正名芡实,因肇庆所产之芡实颗粒大、药力强,故名。”某科研所为进一步改良肇实,为此对肇实的两个品种(分别称为品种A和品种B)进行试验.选取两大片水塘,每大片水塘分成n小片水塘,在总共2n小片水塘中,随机选n小片水塘种植品种A,另外n小片水塘种植B.
(1)假设n=4,在第一大片水塘中,种植品种A的小片水塘的数目记为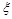 ,求
,求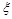 的分布列和数学期望;
的分布列和数学期望;
(2)试验时每大片水塘分成8小片,即n=8,试验结束后得到品种A和品种B在每个小片水塘上的每亩产量(单位:kg/亩)如下表:
| 号码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 品种A | 101 | 97 | 92 | 103 | 91 | 100 | 110 | 106 |
| 品种B | 115 | 107 | 112 | 108 | 111 | 120 | 110 | 113 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
中国航母“辽宁舰”是中国第一艘航母,“辽宁”号以4台蒸汽轮机为动力,为保证航母的动力安全性,科学家对蒸汽轮机进行了170余项技术改进,增加了某项新技术,该项新技术要进入试用阶段前必须对其中的三项不同指标甲、乙、丙进行通过量化检测.假如该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为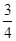 、
、 、
、 .指标甲、乙、丙合格分别记为4分、2分、4分;若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响.
.指标甲、乙、丙合格分别记为4分、2分、4分;若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响.
(I)求该项技术量化得分不低于8分的概率;
(II)记该项新技术的三个指标中被检测合格的指标个数为随机变量X,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对关于 的一元二次方程
的一元二次方程 ……
…… ,解决下列两个问题:
,解决下列两个问题:
(1)若 是从
是从 三个数中任取的一个数,
三个数中任取的一个数, 是从
是从 三个数中任取的一个数,求方程
三个数中任取的一个数,求方程 有两个不相等实根的概率;
有两个不相等实根的概率;
(2)若 是从区间
是从区间 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求方程
任取的一个数,求方程 有两个不相等实根的概率.
有两个不相等实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某食品加工厂甲,乙两个车间包装小食品,在自动包装传送带上每隔30分钟抽取一袋食品,称其重量并将数据记录如下:
甲:102 100 98 97 103 101 99
乙: 102 101 99 98 103 98 99
(1)食品厂采用的是什么抽样方法(不必说明理由)?
(2)根据数据估计这两个车间所包装产品每袋的平均质量;
(3)分析哪个车间的技术水平更好些?
附: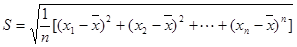
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了防止受污染的产品影响我国民众的身体健康,要求产品在进入市场前必须进行两轮检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为 ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为 ,两轮检测是否合格相互没有影响.
,两轮检测是否合格相互没有影响.
(Ⅰ)求该产品不能销售的概率;
(Ⅱ)如果产品可以销售,则每件产品可获利40元;如果产品不能销售,则每件产品亏损80元(即获利-80元).已知一箱中有产品4件,记一箱产品获利X元,求X的分布列,并求出均值E(X).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com