
| A. | (0,$\frac{1}{2}$) | B. | (-∞,0)∪($\frac{1}{2}$,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | ($\frac{1}{2}$,$\frac{\sqrt{2}+1}{4}$] |
分析 根据一元二次方程根的个数与△的关系,结合韦达定理,可得关于x的方程2ax2-x+2a-1=0的两根均为正实数时,$\left\{\begin{array}{l}a≠0\\△=1-8a(2a-1)≥0\\ \frac{1}{2a}>0\\ \frac{2a-1}{2a}>0\end{array}\right.$,解得实数a的取值范围.
解答 解:若关于x的方程2ax2-x+2a-1=0的两根均为正实数,
则$\left\{\begin{array}{l}a≠0\\△=1-8a(2a-1)≥0\\ \frac{1}{2a}>0\\ \frac{2a-1}{2a}>0\end{array}\right.$,
解得:a∈($\frac{1}{2}$,$\frac{\sqrt{2}+1}{4}$],
故选:D
点评 本题考查的知识点是一元二次方程根的分布与系数的关系,难度不大,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
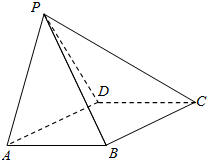 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠DAB=60°,AB=2,△PAD为等边三角形,平面PAD⊥平面ABCD.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠DAB=60°,AB=2,△PAD为等边三角形,平面PAD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 当天处罚金额x(单位:元) | 0 | 5 | 10 | 15 | 20 |
| 当天闯红灯的人数y | 80 | 50 | 40 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>0且b2-4ac>0 | B. | -$\frac{b}{2a}$>0 | C. | b2-4ac>0 | D. | -$\frac{b}{2a}<0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com