
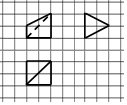
 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )| A. | 8π | B. | $\frac{25}{2}$π | C. | 12π | D. | $\frac{41}{4}$π |
分析 根据三视图得出空间几何体是镶嵌在正方体中的四棱锥O-ABCD,正方体的棱长为2,A,D为棱的中点,利用球的几何性质求解即可.
解答  解:根据三视图得出:该几何体是镶嵌在正方体中的四棱锥O-ABCD,正方体的棱长为2,A,D为棱的中点
解:根据三视图得出:该几何体是镶嵌在正方体中的四棱锥O-ABCD,正方体的棱长为2,A,D为棱的中点
根据几何体可以判断:球心应该在过A,D的平行于底面的中截面上,
设球心到截面BCO的距离为x,则到AD的距离为:2-x,
∴R2=x2+($\sqrt{2}$)2,R2=12+(2-x)2,
解得出:x=$\frac{3}{4}$,R=$\frac{\sqrt{41}}{4}$,
该多面体外接球的表面积为:4πR2=$\frac{41}{4}$π,
故选D.
点评 本题综合考查了空间几何体的性质,学生的空间思维能力,构造思想,关键是镶嵌在常见的几何体中解决.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:选择题
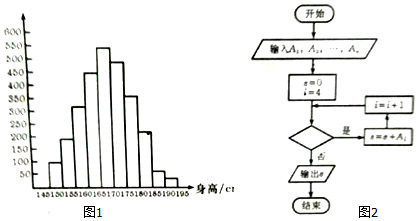
| A. | i<6 | B. | i<7 | C. | i<8 | D. | i<9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1)n-1$\frac{1}{{3}^{n}}$ | B. | (-1)n-1$\frac{1}{3n}$ | C. | (-1)n$\frac{1}{{3}^{n}}$ | D. | (-1)n$\frac{1}{3n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
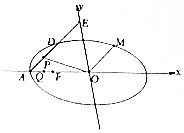 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{12}$=1(a>2$\sqrt{3}$)的左焦点为F,左顶点为A,$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$,其中O为原点,e为椭圆的离心率,过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{12}$=1(a>2$\sqrt{3}$)的左焦点为F,左顶点为A,$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$,其中O为原点,e为椭圆的离心率,过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4或3 | B. | -$\frac{3}{7}$ | C. | -3 | D. | -4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com