
【题目】把函数y=sin(2x+![]() )的图象向右平移
)的图象向右平移![]() 个单位,再把所得图象上各点的横坐标缩短到原来的
个单位,再把所得图象上各点的横坐标缩短到原来的![]() , 则所得图象的函数解析式是( )
, 则所得图象的函数解析式是( )
A.y=sin(4x+![]() π)
π)
B.y=sin(4x+![]() )
)
C.y=sin4x
D.y=sinx
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系![]() 的坐标平面
的坐标平面![]() 内,若函数
内,若函数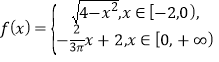 的图象与
的图象与![]() 轴围成一个封闭区域
轴围成一个封闭区域![]() ,将区域
,将区域![]() 沿
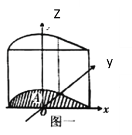
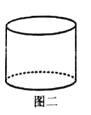
沿![]() 轴的正方向上移4个单位,得到几何体如图一.现有一个与之等高的圆柱如图二,其底面积与区域
轴的正方向上移4个单位,得到几何体如图一.现有一个与之等高的圆柱如图二,其底面积与区域![]() 面积相等,则此圆柱的体积为( )
面积相等,则此圆柱的体积为( )
A. ![]() B.
B. ![]() C. 2
C. 2![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x+2|﹣|x﹣1|
(I)画出函数y=f(x)的图象;
(II)若关于x的不等式f(x)+4≥|1﹣2m|有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解放军某部在实兵演练对抗比赛中,红、蓝两个小组均派6人参加实弹射击,其所得成绩的茎叶图如图所示.
(1)根据射击数据,计算红、蓝两个小组射击成绩的均值与方差,并说明红军还是蓝军的成绩相对比较稳定;
(2)若从蓝军6名士兵中随机抽取两人,求所抽取的两人的成绩之差不超过2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知AB为半圆O的直径,AB=4,C为半圆上一点,过点C作半圆的切线CD,过点A作AD⊥CD于D,交半圆于点E,DE=1.
(Ⅰ)求证:AC平分∠BAD;
(Ⅱ)求BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学在校就餐的高一年级学生有440名,高二年级学生有460名,高三年级学生有500名;为了解学校食堂的服务质量情况,用分层抽样的方法从中抽取70名学生进行抽样调查,把学生对食堂的“服务满意度”与“价格满意度”都分为五个等级:1级(很不满意);2级(不满意);3级(一般);4级(满意);5级(很满意),其统计结果如下表(服务满意度为x,价格满意度为y).
y | 价格满意度 | |||||
1 | 2 | 3 | 4 | 5 | ||
服 | 1 | 1 | 1 | 2 | 2 | 0 |
2 | 2 | 1 | 3 | 4 | 1 | |
3 | 3 | 7 | 8 | 8 | 4 | |
4 | 1 | 4 | 6 | 4 | 1 | |
5 | 0 | 1 | 2 | 3 | 1 | |
(1)求高二年级共抽取学生人数;
(2)求“服务满意度”为3时的5个“价格满意度”数据的方差;
(3)为提高食堂服务质量,现从x<3且2≤y<4的所有学生中随机抽取两人征求意见,求至少有一人的“服务满意度”为1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣3ax(a∈R)
(1)当a=1时,求f(x)的极小值;
(2)若直线x+y+m=0对任意的m∈R都不是曲线y=f(x)的切线,求a的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com