
| A. | (-3,0)∪(3,+∞) | B. | (-∞,-3)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-3,0)∪(0,3) |
分析 易判断f(x)在(-∞,0)上的单调性及f(x)图象所过特殊点,作出f(x)的草图,根据图象可解不等式.
解答 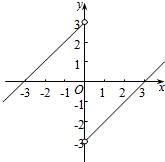 解:∵f(x)在R上是奇函数,且f(x)在(0,+∞)上是增函数,
解:∵f(x)在R上是奇函数,且f(x)在(0,+∞)上是增函数,
∴f(x)在(-∞,0)上也是增函数,
由f(3)=0,得f(-3)=-f(3)=0,
即f(-3)=0,
作出f(x)的草图,如图所示:
由图象,得xf(x)<0?$\left\{\begin{array}{l}{x>0}\\{f(x)<0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{f(x)>0}\end{array}\right.$,
解得0<x<3或-3<x<0,
∴xf(x)<0的解集为:(-3,0)∪(0,3),
故选:D.
点评 本题考查函数奇偶性、单调性的综合应用,考查数形结合思想,灵活作出函数的草图是解题关键.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{4\sqrt{3}}{3}$ | C. | 2 | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
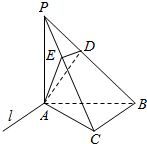 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.平面ADE∩平面ABC=l.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.平面ADE∩平面ABC=l.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | B⊆A | ||
| C. | A∩B=∅ | D. | 集合A、B间没有包含关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com